题目内容
已知矩阵M=
.
(Ⅰ)请写出矩阵M对应的变换f的变换公式;
(Ⅱ)从变换的角度说明矩阵M可逆吗?如果可逆,请用求逆变换的方式求出对应的逆矩阵M-1.
|
(Ⅰ)请写出矩阵M对应的变换f的变换公式;
(Ⅱ)从变换的角度说明矩阵M可逆吗?如果可逆,请用求逆变换的方式求出对应的逆矩阵M-1.
考点:变换、矩阵的相等,逆变换与逆矩阵
专题:矩阵和变换
分析:本题(Ⅰ)利用矩阵与向量积的运算法则可以得出结论;(Ⅱ)利用向量变换的几何意义可以写出逆矩阵.
解答:
解:(Ⅰ)假设M=
把任一点(x,y)变成(x',y'),
则
=
∴
.
(Ⅱ)从变换的角度看,变换f是可逆的.由(Ⅰ)得矩阵M对应的变换f是y轴方向上的切变变换.因为变换f把每个点在横坐标不变的情况下,纵坐标变为原来纵坐标加上横坐标的2倍,所以它的逆变换f-1应该是把每个点在横坐标不变的情况下,纵坐标变为原来纵坐标减去横坐标的2倍.
∴
,
∴M-1=
.
|
则
|
|
|
|
(Ⅱ)从变换的角度看,变换f是可逆的.由(Ⅰ)得矩阵M对应的变换f是y轴方向上的切变变换.因为变换f把每个点在横坐标不变的情况下,纵坐标变为原来纵坐标加上横坐标的2倍,所以它的逆变换f-1应该是把每个点在横坐标不变的情况下,纵坐标变为原来纵坐标减去横坐标的2倍.
∴
|
∴M-1=
|
点评:本题考查了矩阵与向量的乘法、逆矩阵的求法,本题在求逆矩阵时,还可以采用定义法或公式法加以研究.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
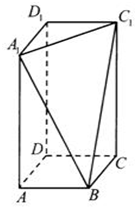 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为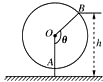 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h. 如图,已知三棱锥P-ABC,平面PAC⊥平面ABC,AB=BC=CA=4,PA=2
如图,已知三棱锥P-ABC,平面PAC⊥平面ABC,AB=BC=CA=4,PA=2