题目内容

已知函数f（x）是R上的可导函数，且f′（1）=2，则
lim
h→0
f(1+h)-f(1)
h
=
 
．
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：根据导数的定义即可求出
解答： 解：∵函数f（x）是R上的可导函数，
∴
lim
h→0
f(1+h)-f(1)
h
=f′（1）=2．
故答案为：2．
点评：本题主要考查了导数的定义，属于基础题．
练习册系列答案
相关题目
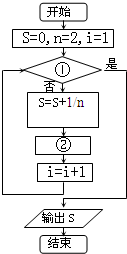
如图给出了计算
1
2
+
1
4
+
1
6
+…+
1
60
的值的程序框图，其中①②分别是（　　）
A、i＜30，n=n+2
B、i=30，n=n+2
C、i＞30，n=n+2
D、i＞30，n=n+1
设函数f（x）=x3-
3
2
ax2+a（a∈R）．
（Ⅰ）讨论函数f（x）的单调区间；
（Ⅱ）求函数f（x）在区间[0，2]上的最小值；
（Ⅲ）是否存在实数a使得函数f（x）在区间（-1，2）上既存在最大值又存在最小值，若存在，求出a的取值范围；若不存在，说明理由．
通过随机调查我校高三100名学生在高二文理分科是否与性别有关，得到如下的列联表：（单位：人）
性别\
理\
文		 男 女 总计
选理科 40 20 60
选文科 10 30 40
总计 50 50 100
（1）从这50名女生中按文理采取分层抽样，抽取一个容量为5的样本，问样本中文科生与理科生各多少人？
（2）从（1）中抽到的5名女生中随机选取两名访谈，求选到文科生、理科生各一名的概率；
（3）根据以上列联表；问有多大把握认为“文理分科与性别”有关？
统计量k2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d
概率表：
P（k2≥k0） 0.15 0.10 0.05 0.025 0.010
k0 2.072 2.706 3.841 5.024 6.635
设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1、F2，椭圆的离心率为
1
2
，连接椭圆的四个顶点得到的菱形面积为4
3
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过右焦点F2作斜率为K的直线L与椭圆C交M、N两点，在y轴上是否存在点P（0，m）使得以PM，PN为邻边的平行四边形是菱形，如果存在，求出m的取值范围，如果不存在，说明理由．
曲线y=-lnx在点（1，0）处的切线斜率为
 
．
为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组及各组的频数如表．根据以上数表绘制相应的频率分布直方图时，落在[10.95，11.15）范围内的矩形的高应为
 
．
分组 频数
[10.75，11.95） 12
[10.95，11.15） 29
[11.15，11.35） 46
[11.35，11.55） 11
[11.55，11.75） 2
已知向量
a
，
b
，满足|
a
|=1，|
b
|=
3
，
a
+
b
=（
3
，1），则向量
a
+
b
与向量
a
-
b
的夹角是
 
．
若直线y=kx+2k与圆x2+y2+mx+4=0至少有一个交点，则实数m的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网