题目内容
12.曲线C:$\left\{\begin{array}{l}{x=secθ}\\{y=tanθ}\end{array}\right.$(θ为参数)的两个顶点之间的距离为2.分析 根据题意,将曲线的参数方程变形为普通方程,分析可得曲线C为双曲线,且两个顶点的坐标为(±1,0),由两点间距离公式计算可得答案.
解答 解:曲线C:$\left\{\begin{array}{l}{x=secθ}\\{y=tanθ}\end{array}\right.$,其普通方程为x2-y2=1,
则曲线C为双曲线,且两个顶点的坐标为(±1,0),
则则两个顶点之间的距离为2;
故答案为:2.
点评 本题考查参数方程与普通方程的互化,涉及双曲线的几何性质,关键是将曲线的参数方程化为普通方程.

练习册系列答案
相关题目
3.关于残差和残差图,下列说法正确的是( )
(1)残差就是随机误差
(2)残差图的纵坐标是残差
(3)残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越高
(4)残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越低.
(1)残差就是随机误差
(2)残差图的纵坐标是残差
(3)残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越高
(4)残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越低.
| A. | (1)(2) | B. | (3)(4) | C. | (2)(3) | D. | (2)(4) |
20.已知数列{an}满足a1=4,an+1=an+2n,设bn=$\frac{{a}_{n}}{n}$,若存在正整数T,使得对一切n∈N*,bn≥T恒成立,则T的最大值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
4.两座灯塔A和B与海洋观察站C的距离分别为10km和20km,灯塔A在观察站C的北偏东15°方向上,灯塔B在观察站C的南偏西75°方向上,则灯塔A与灯塔B的距离为( )
| A. | 10$\sqrt{5}$km | B. | 10$\sqrt{7}$km | C. | 10$\sqrt{3}$km | D. | 30km |
1.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移$\frac{π}{2}$个单位,沿y轴向下平移1个单位,得到函数y=$\frac{1}{2}$sinx的图象,则y=f(x)的解析式为( )
| A. | y=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)+1 | B. | y=$\frac{1}{2}$sin(2x-$\frac{π}{2}$)+1 | C. | y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$)+1 | D. | y=$\frac{1}{2}$sin($\frac{1}{2}$x-$\frac{π}{4}$)+1 |
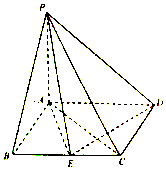 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.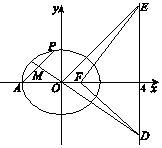 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.