题目内容
1.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移$\frac{π}{2}$个单位,沿y轴向下平移1个单位,得到函数y=$\frac{1}{2}$sinx的图象,则y=f(x)的解析式为( )| A. | y=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)+1 | B. | y=$\frac{1}{2}$sin(2x-$\frac{π}{2}$)+1 | C. | y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$)+1 | D. | y=$\frac{1}{2}$sin($\frac{1}{2}$x-$\frac{π}{4}$)+1 |
分析 利用y=Asin(ωx+φ)的图象变换规律,求得f(x)的解析式.
解答 解:由题意可得,把函数y=$\frac{1}{2}$sinx的图象沿y轴向上平移1个单位,
可得函数y=$\frac{1}{2}$sinx+1的图象;
再将整个图象沿x轴向左平移$\frac{π}{2}$个单位,可得函数y=$\frac{1}{2}$sin(x+$\frac{π}{2}$)+1的图象;
再把横坐标变为原来的$\frac{1}{2}$倍,可得函数y=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)+1=f(x)的图象,
故选:A.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.高二(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本,已知学号为8,22,50的同学在样本中,那么还有一个同学的学号应为( )
| A. | 32 | B. | 33 | C. | 35 | D. | 36 |
8.数列{an}中,已知a1=1,a2=2,an+2=an+1-an(n∈N*),则a2017=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |

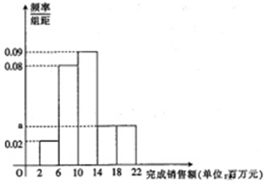 某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.
某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.