题目内容
已知数列{an}的前n项和Sn=n2(n∈N*).设数列{
}的前n项和为Tn.
(Ⅰ)求Tn;
(Ⅱ)求正整数m,n (m≠n),使得T1,Tm,Tn成等比数列.
| 1 |
| anan+1 |
(Ⅰ)求Tn;
(Ⅱ)求正整数m,n (m≠n),使得T1,Tm,Tn成等比数列.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)根据题意和当n≥2时an=Sn-Sn-1化简,再验证a1=S1,求出an代入
化简,利用裂项相消法求出数列{
}的前n项和为Tn;
(Ⅱ)由(I)化简Tn,根据等比中项的性质得
=T1•Tn,化简后求出m的范围,再由m,n (m≠n)取正整数,求出m、n的值.
| 1 |
| anan+1 |
| 1 |
| anan+1 |
(Ⅱ)由(I)化简Tn,根据等比中项的性质得
| T | 2 m |
解答:
解:(Ⅰ)由题意得,数列{an}的前n项和Sn=n2(n∈N*),
所以当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
又a1=S1=1,故an=2n-1 (n∈N*),
所以
=
=
(
-
),
则Tn=
[(1-
)+(
-
)+…+((
-
))]
=
(1-
)=
; …(5分)
(Ⅱ)假设正整数m,n (m≠n),使得T1,Tm,Tn成等比数列.
由(I)得,Tn=
=
(n∈N*),所以{Tn}是递增数列,
由
=T1•Tn 得,(2+
)2=
(
)=6+
>6,故2+
>
,
又m≠n,所以1<m<
( m∈N*),
即m=2,解得n=12.
所以当m=2,n=12时,T1,Tm,Tn成等比数列. …(15分)
所以当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
又a1=S1=1,故an=2n-1 (n∈N*),
所以
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
(Ⅱ)假设正整数m,n (m≠n),使得T1,Tm,Tn成等比数列.
由(I)得,Tn=
| n |
| 2n+1 |
| 1 | ||
2+
|
由
| T | 2 m |
| 1 |
| m |
| 1 |
| 3 |
| 1 | ||
2+
|
| 3 |
| n |
| 1 |
| m |
| 6 |
又m≠n,所以1<m<
2+
| ||
| 2 |
即m=2,解得n=12.
所以当m=2,n=12时,T1,Tm,Tn成等比数列. …(15分)
点评:本题考查数列an与Sn的关系式,等比中项的性质,以及裂项相消法求数列的和,同时考查运算求解能力.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知集合A={3,4},则A的子集个数为( )
| A、16 | B、15 | C、4 | D、3 |
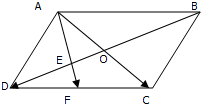 如图所示,已知?ABCD,E是OD的中点,
如图所示,已知?ABCD,E是OD的中点,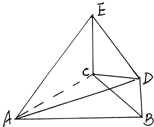 如图,EC⊥平面ABC,EC∥BD,平面ACD⊥平面ECB.
如图,EC⊥平面ABC,EC∥BD,平面ACD⊥平面ECB.