题目内容
已知a
+a -
=3(a>0),求
的值.
| 1 |
| 2 |
| 1 |
| 2 |
a
| ||||
a
|
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:令a
=m>0,a-
=n>0,a
+a -
=3(a>0),可得m+n=3.再利用立方差公式即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:令a
=m>0,a-
=n>0,
∵a
+a -
=3(a>0),∴m+n=3.
∴
=
=m2+mn+n2=(m+n)2-mn=32-1=8.
| 1 |
| 2 |
| 1 |
| 2 |
∵a
| 1 |
| 2 |
| 1 |
| 2 |
∴
a
| ||||
a
|
| m3-n3 |
| m-n |
点评:本题考查了指数运算法则、乘法公式,考查了计算能力,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
如果函数y=-2x+k的图象与方程x|x|+
=1的曲线恰好有两个公共点,则实数k的值是( )
| y|y| |
| 4 |
A、[0,2
| ||
B、[0,2
| ||
C、(0,2
| ||
| D、(0,2] |
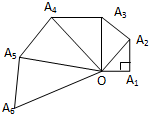 如图OA1=1,直角三角形OAnAn+1(n=1,2,3…)的直角边AnAn+1=
如图OA1=1,直角三角形OAnAn+1(n=1,2,3…)的直角边AnAn+1=| n |
A、an=
| ||||
B、an=
| ||||
C、an=
| ||||
D、an=
|
已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )
| A、AB∥m | B、AC⊥m |
| C、AC⊥β | D、AB∥β |