题目内容
20.直线$\left\{\begin{array}{l}x=1+\frac{4}{5}t\\ y=-1+\frac{3}{5}t\end{array}\right.$(t为参数)被曲线ρ=$\sqrt{2}$cos(θ+$\frac{π}{4}$)所截的弦长为( )| A. | $\frac{1}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{7}{5}$ | D. | $\frac{5}{7}$ |
分析 直线$\left\{\begin{array}{l}x=1+\frac{4}{5}t\\ y=-1+\frac{3}{5}t\end{array}\right.$(t为参数),消去参数t化为普通方程.曲线ρ=$\sqrt{2}$cos(θ+$\frac{π}{4}$),利用ρ2=x2+y2,x=ρcosθ,y=ρsinθ,可得直角坐标方程.求出圆心到直线的距离,可得直线被曲线C所截的弦长.
解答 解:直线$\left\{\begin{array}{l}x=1+\frac{4}{5}t\\ y=-1+\frac{3}{5}t\end{array}\right.$(t为参数),消去参数化为:3x-4y-7=0.
曲线ρ=$\sqrt{2}$cos(θ+$\frac{π}{4}$)即ρ2=ρcosθ-ρsinθ,化为直角坐标方程:x2+y2=x-y,
配方为:(x-$\frac{1}{2}$)2+(y+$\frac{1}{2}$)2=$\frac{1}{2}$,可得圆心C($\frac{1}{2}$,-$\frac{1}{2}$),半径r=$\frac{\sqrt{2}}{2}$.
圆心到直线的距离d=$\frac{|\frac{3}{2}+2-7|}{5}$=$\frac{7}{10}$,可得直线被曲线C所截的弦长为=2$\sqrt{\frac{1}{2}-\frac{49}{100}}$=$\frac{1}{5}$.
故选:A.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、直线与圆相交弦长问题,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.若集合A={0,1},B={y|y=2x,x∈A},则(∁RA)∩B=( )
| A. | {0} | B. | {2} | C. | {2,4} | D. | {0,1,2} |
11.某研究机构对高三学生的记忆力x和判断力y进行统计分析,得到下表数据
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)试根据(2)中求出的线性回归方程,预测记忆力为9的同学的判断力.
(相关公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x,参考数据$\sum_{i=1}^{4}$xiyi=158,$\sum_{i=1}^{4}$x${\;}_{i}^{2}$=344)
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)试根据(2)中求出的线性回归方程,预测记忆力为9的同学的判断力.
(相关公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x,参考数据$\sum_{i=1}^{4}$xiyi=158,$\sum_{i=1}^{4}$x${\;}_{i}^{2}$=344)
9.在△ABC中,“A=$\frac{π}{4}$”是“sinA=$\frac{\sqrt{2}}{2}$”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分也非必要条件 |
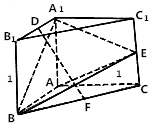 已知三棱柱ABC-A1B1C1中,底面三角形ABC是直角三角形,四边形A1ACC1和四边形A1ABB1均为正方形,D,E,F分别是A1B1,C1C,BC的中点,AB=1.
已知三棱柱ABC-A1B1C1中,底面三角形ABC是直角三角形,四边形A1ACC1和四边形A1ABB1均为正方形,D,E,F分别是A1B1,C1C,BC的中点,AB=1.