题目内容
函数f(x)=sinx,x∈(α,β),且(α,β)⊆[0,π],若任意x1,x2,x3∈(α,β),f(x1),f(x2),f(x3)都能构成某个三角形的三条边,则β-α的最大值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
考点:正弦定理
专题:三角函数的图像与性质
分析:令f(x3)的值最大,根据f(x1)+f(x2)>f(x3)=1,根据正弦函数图象进行推断.
解答:
解:令f(x3)的值最大,当x3=
,f(x3)=1,为最大值,
∵f(x1),f(x2),f(x3)都能构成某个三角形的三条边,
∴f(x1)+f(x2)>f(x3),即f(x1)+f(x2)>1,

当x1,x2在直线y=
的上方时满足条件,
故β-α的最大值为
-
=
,
故选:C.
| π |
| 2 |
∵f(x1),f(x2),f(x3)都能构成某个三角形的三条边,
∴f(x1)+f(x2)>f(x3),即f(x1)+f(x2)>1,

当x1,x2在直线y=
| 1 |
| 2 |
故β-α的最大值为
| 5π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
故选:C.
点评:本题主要考查了三角函数图象与性质.考查了学生分析和推理的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
椭圆
+
=1(a>b>0)的左右焦点分别为F1,F2,若其上存在一点Q使得∠F1QF2=120°,则其离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(0,1) | ||||
B、[
| ||||
C、[
| ||||
D、[
|
通过随机询问250名不同性别的大学生在购买食物时是否看营养说明书,得到如下2×2联表:
从调查的结果分析,认为性别和读营养说明书的关系( )
| 女 | 男 | 总计 | |
| 读营养说明书 | 90 | 60 | 150 |
| 不读营养说明书 | 30 | 70 | 100 |
| 总计 | 120 | 130 | 250 |
| A、95%以上认为无关 |
| B、90%~95%认为有关 |
| C、95%~99.9%认为有关 |
| D、99.9%以上认为有关 |
方程x2+y2-2x+4y+6=0表示的曲线是( )
| A、圆 | B、点 | C、不存在 | D、无法确定 |
已知集合A={x|y=
},B={x∈Z|-2≤x≤4},则A∩B等于( )
| x |
| A、{0,1,2,3,4} |
| B、{x|0≤x≤4} |
| C、{-2,-1,0,1,2,3,4} |
| D、{2,3,4} |
函数f(x)在定义域R内可导,若对x∈R,恒有f(1+x)=f(1-x),且当x∈(-∞,1)时,(x-1)f′(x)<0,设a=f(0),b=f(
),c=f(3),则( )
| 1 |
| 2 |
| A、b<c<a |
| B、c<a<b |
| C、c<b<a |
| D、a<b<c |
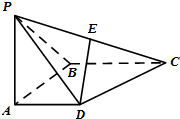 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.