题目内容
计算:
(1)lg25+lg2lg50;
(2)已知a+a-1=3,求a2+a-2和a
+a-
的值.
(1)lg25+lg2lg50;
(2)已知a+a-1=3,求a2+a-2和a
| 1 |
| 2 |
| 1 |
| 2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用对数的运算法则及其lg2+lg5=1即可得出;
(2)利用指数的运算法则及其乘法公式即可得出.
(2)利用指数的运算法则及其乘法公式即可得出.
解答:
解:(1)原式=lg25+lg2•lg(5×10)
=lg25+lg2•(lg5+1)
=lg5(lg5+lg2)+lg2
=lg5+lg2=1.
(2)∵a+a-1=3,
∴a2+a-2=(a+a-1)2-2=7,
∵a
+a-
>0,
(a
+a-
)2=a+a-1+2=5,
∴a
+a-
=
.
=lg25+lg2•(lg5+1)
=lg5(lg5+lg2)+lg2
=lg5+lg2=1.
(2)∵a+a-1=3,
∴a2+a-2=(a+a-1)2-2=7,
∵a
| 1 |
| 2 |
| 1 |
| 2 |
(a
| 1 |
| 2 |
| 1 |
| 2 |
∴a
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
点评:本题考查了对数的运算法则及其lg2+lg5=1、指数的运算法则及其乘法公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知A={x|0≤x≤3},B={y|0≤y≤3},下列从集合A到集合B的对应关系不是映射的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
下列函数中,与函数y=x相同的函数是( )
A、y=
| ||||
B、y=(
| ||||
| C、y=lg10x | ||||
| D、y=2log2x |
若函数f(x)=(m2-m-1)xm是幂函数,则f(x)一定( )
| A、是偶函数 |
| B、是奇函数 |
| C、在x∈(-∞,0)上单调递减 |
| D、在x∈(0,+∞)上单调递减 |
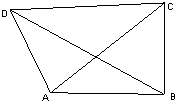 如图:在平面四边形ABCD中,AB=3
如图:在平面四边形ABCD中,AB=3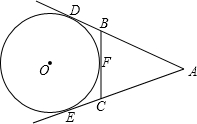 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为