题目内容
用适当的方法表示下列集合：
（1）直角坐标系中横坐标为1的点的集合；
（2）满足不等式1＜1+3x＜26的奇数组成的集合．
（1）直角坐标系中横坐标为1的点的集合；
（2）满足不等式1＜1+3x＜26的奇数组成的集合．
考点：集合的表示法
专题：集合
分析：根据集合的表示法，根据题意描述即可．
解答：
解：（1）{（x，y）|x=1，y∈R}，
（2）∵1＜1+3x＜26，
解得0＜x＜
，
∵x为奇数，
∴x=1，3，5，7，
∴满足不等式1＜1+3x＜26的奇数组成的集合为{1，3，5，7}
（2）∵1＜1+3x＜26，
解得0＜x＜
| 25 |
| 3 |
∵x为奇数，
∴x=1，3，5，7，
∴满足不等式1＜1+3x＜26的奇数组成的集合为{1，3，5，7}
点评：此题是个基础题．本题考查描述法表示集合，抓住描述法的特征表示即可．
练习册系列答案
相关题目
定义：如果函数f（x）在[a，b]上存在x1，x2（a＜x1＜x2＜b），满足f′（x1）=
，f（x）=f′（x2）=
，则称数x1，x2为[a，b]上的“对望数”，函数f（x）为[a，b]上的“对望函数”．已知函数f（x）=
x3-x2+m是[0．m]上的“对望函数”，则实数m的取值范围是（ ）
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
| 1 |
| 3 |
A、（1，
| ||||
B、（
| ||||
| C、（1，2）∪（2，3） | ||||
D、（1，
|
若复数z满足z（3-4i）=5，则z的虚部为（ ）
A、-
| ||
B、
| ||
| C、-4 | ||
| D、4 |
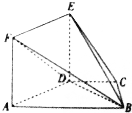如图，在多面体ABCDEF中，平面ADEF⊥平面ABCD，AB∥DC，ADEF是正方形，已知BD=2AD=2，AB=2DC=
如图，四棱锥P-ABCD中，PA=CA，PA⊥底面ABCD，E，F，分别为PD，PC的中点，且底面ABCD中，∠ABC，∠ACD都为直角，∠BAC，∠CAD的大小都为60°．
某校从参加某次数学能力测试的学生中中抽查36名学生，统计了他们的数学成绩（成绩均为整数且满分为120分），成绩的频率直方图如图所示，