题目内容

2．已知全集U=R，集合A={x|2≤x＜7}，B={x|0＜log3x＜2}，C={x|a＜x＜a+1}．
（1）求A∪B，（∁UA）∩B；
（2）如果A∩C=∅，求实数a的取值范围．

分析 （1）分别求出集合A，集合B，从而求出A∪B，∁RA，B∩（∁RA）；
（2）通过C是非空集合，A∩C=∅，而a+1≤2或a≥7，从而求出a的范围．

解答 解：（1）由0＜log3x＜2，得1＜x＜9∴B=（1，9），
∵A={x|2≤x＜7}=[2，7），
∴A∪B=（1，9）
∁UA=（-∞，2）∪[7，+∞），
∴（∁UA）∩B=（1，2）∪[7，9）
（2）C={x|a＜x＜a+1}=（a，a+1）
∵A∩C=∅，
∴a+1≤2或a≥7，解得：a≤1或a≥7

点评 本题考查了对数函数的单调性的运用以及集合的运算，关键是正确化简集合，然后由进行集合的运算，属于基础题．

练习册系列答案
相关题目
12．已知A（-3，0），B（0，4），点P为直线y=x上一点，过A，B，P三点的圆记作圆C，则“点P为原点”是“圆C的半径取得最小值”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．计算（$\frac{8}{125}$）${\;}^{-\frac{2}{3}}$-lg$\sqrt{2}$-lg$\sqrt{5}$的结果为$\frac{23}{4}$．
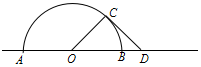10．某公园内直线道路旁有一半径为10米的半圆形荒地（圆心O在道路上，AB为直径），现要在荒地的基础上改造出一处景观．在半圆上取一点C，道路上B点的右边取一点D，使OC垂直于CD，且OD的长不超过20米．在扇形区域AOC内种植花卉，三角形区域OCD内铺设草皮．已知种植花卉的费用每平方米为200元，铺设草皮的费用每平方米为100元．
（1）设∠COD=x（单位：弧度），将总费用y表示为x的函数式，并指出x的取值范围；
（2）当x为何值时，总费用最低？并求出最低费用．
17．将正弦曲线y=sinx上所有的点向右平移$\frac{2}{3}$π个单位长度，再将图象上所有点的横坐标变为原来的$\frac{1}{3}$倍（纵坐标不变），则所得到的图象的函数解析式y=$sin（3x-\frac{2π}{3}）$．
7．直线$\frac{x}{a}-\frac{y}{b}=1$在y轴上的截距是（　　）
A．aB．bC．-aD．-b
14．数列{an}中，已知a1=1，若${a_n}-{a_{n-1}}=2（n≥2且n∈{N^*}）$，则an=2n-1，若$\frac{a_n}{{{a_{n-1}}}}=2（n≥2且n∈{N^*}）$，则an=2n-1．
11．已知函数f（x）=ax-1（a＞0且a≠1）的图象过定点A，则点A为（　　）
A．（0，-1）B．（0，1）C．（-1，1）D．（1，1）
12．已知函数f（x）=ex，g（x）=-x2+2x-af（x）（a∈R），x1，x2是两个任意实数且x1≠x2．
（1）求函数f（x）的图象在x=0处的切线方程；
（2）若函数g（x）在R上是增函数，求a的取值范围；
（3）求证：$f（\frac{{{x_1}+{x_2}}}{2}）＜\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网