题目内容
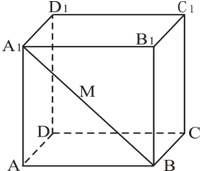
如图，正方体ABCD-A1B1C1D1的棱长为1，点M是面对角线A1B上的动点，则AM+MD1的最小值为 ．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：把对角面A1C绕A1B旋转，使其与△AA1B在同一平面上，连接AD1并求出，根据平面内两点之间线段最短，可知就是最小值．
解答：
解：把对角面A1C绕A1B旋转，使其与△AA1B在同一平面上，连接AD1，
则在△AA1D中，AD1=
=
为所求的最小值．
故答案为：
解：把对角面A1C绕A1B旋转，使其与△AA1B在同一平面上，连接AD1，则在△AA1D中，AD1=
| 1+1-2×1×1×cos135° |
2+
|
故答案为：
2+
|
点评：本题的考点是点、线、面间的距离计算，主要考查考查棱柱的结构特征，考查平面内两点之间线段，最短考查计算能力，空间想象能力，基本知识的考查．
练习册系列答案
相关题目
已知△ABC的三边长BC=a，AC=b，AB=c，O为△ABC所在平面内一点，若a
+b
+c
=
，则点O是△ABC的（ ）
| OA |
| OB |
| OC |
| 0 |
| A、外心 | B、内心 | C、重心 | D、垂心 |