题目内容
已知数列{an}的前n项和为Sn,a1=3且an+1=2Sn+3;数列{bn}为等差数列,且公差d>0,b1+b2+b3=15.
(1)求数列{an}的通项公式;
(2)若
+b1,
+b2,
+b3成等比数列,记数列{bn}的前n项和为Tn,求证:
+
+…+
<
.
(1)求数列{an}的通项公式;
(2)若
| a1 |
| 3 |
| a2 |
| 3 |
| a3 |
| 3 |
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
| 3 |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)通过an+1-an=(2Sn+3)-(2Sn-1+3)=2an.利用等比数列的定义判断{an}是公比为3的等比数列.
(2)由题意可求得Tn=3n+
×2=n2+2n,利用裂项法求和,即可得出证明.
(2)由题意可求得Tn=3n+
| n(n-1) |
| 2 |
解答:
解:(1)当n≥2时,an+1-an=(2Sn+3)-(2Sn-1+3)=2an.
∴an+1=3an,即
=3,
又 a2=2S1+3=9=3a1
∴{an}是首项为3,公比为3的等比数列,
∴an=3n;
(2)设{bn}的公差为d(d>0),∵T3=15,∴b2=5,
依题意
+b1,
+b2,
+b3成等比数列,有(
+b2)2=(
+b1)(
+b3),
∴64=(5-d+1)(5+d+9)
d2+8d-20=0,得d=2,或d=-10(舍去),
∴b1=5-2=3
∴Tn=3n+
×2=n2+2n.
∴
=
=
=
(
-
),
∴
+
+…+
=
(1-
+
-
+
-
+…+
-
)=
(1+
-
-
)=
-
(
+
)<
.
∴an+1=3an,即
| an+1 |
| an |
又 a2=2S1+3=9=3a1
∴{an}是首项为3,公比为3的等比数列,
∴an=3n;
(2)设{bn}的公差为d(d>0),∵T3=15,∴b2=5,
依题意
| a1 |
| 3 |
| a2 |
| 3 |
| a3 |
| 3 |
| a2 |
| 3 |
| a1 |
| 3 |
| a3 |
| 3 |
∴64=(5-d+1)(5+d+9)
d2+8d-20=0,得d=2,或d=-10(舍去),
∴b1=5-2=3
∴Tn=3n+
| n(n-1) |
| 2 |
∴
| 1 |
| Tn |
| 1 |
| n2+2n |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
点评:本题考查等差数列,等比数列的性质,等差数列的前n项和,等比关系的确定的应用,考查学生利用裂项相消法求数列的和及计算能力,属于中档题.

练习册系列答案
相关题目
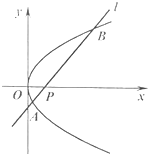 如图,已知抛物线y2=4x,点P(a,0)是x轴上的一点,经过点P且斜率为1的直线l与抛物线相交于A,B两点.
如图,已知抛物线y2=4x,点P(a,0)是x轴上的一点,经过点P且斜率为1的直线l与抛物线相交于A,B两点.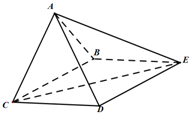 四棱锥A-ABCD中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
四棱锥A-ABCD中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=