题目内容
已知平面上的动点Q到定点F(0,1)的距离与它到定直线y=3的距离相等.
(1)求动点Q的轨迹C1的方程;
(2)过点作直线l1交C2:x2=4y于A,B两点(在第一象限).若|BF|=2|AF|,求直线l1的方程.
(1)求动点Q的轨迹C1的方程;
(2)过点作直线l1交C2:x2=4y于A,B两点(在第一象限).若|BF|=2|AF|,求直线l1的方程.
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设出Q的坐标,根据条件推断出x和y的关系式,化简求得x和y的关系,即曲线的方程.
(2)设出A,B,利用抛物线的定义,表示出|AF|和|BF|,进而利用|BF|=2|AF|,求得y2和y1的关系,令直线AB的方程x=t(y-1),与抛物线方程联立消去x,表示出y1+y2和y1y2,联立求得y1和y2,代入方程②求得t,进而求得t.则直线AB的方程可得.
(2)设出A,B,利用抛物线的定义,表示出|AF|和|BF|,进而利用|BF|=2|AF|,求得y2和y1的关系,令直线AB的方程x=t(y-1),与抛物线方程联立消去x,表示出y1+y2和y1y2,联立求得y1和y2,代入方程②求得t,进而求得t.则直线AB的方程可得.
解答:
解:(1)设Q(x,y),
由条件有
=|y-3|,
化简得曲线C1的方程为:x2=-4y+8.
(2)设A(x1,y1),B(x2,y2),则|AF|=y1+1,|BF|=y2+1,
由|BF|=2|AF|,得y2=2y1+1①
令直线AB方程为x=t(y-1),代入抛物线方程,可得t2y2-(2t2+4)y+t2=0,
∴y1+y2=
②,y1y2=1③
由①和③联立解得:y1=
,y2=2
代入②得:t2=8
依题意直线AB的斜率大于0,即t>0,
∴t=2
故直线AB的方程为x-2
y+2
=0.
由条件有
| x2+(y-1)2 |
化简得曲线C1的方程为:x2=-4y+8.
(2)设A(x1,y1),B(x2,y2),则|AF|=y1+1,|BF|=y2+1,
由|BF|=2|AF|,得y2=2y1+1①
令直线AB方程为x=t(y-1),代入抛物线方程,可得t2y2-(2t2+4)y+t2=0,
∴y1+y2=
| 2t2+4 |
| t2 |
由①和③联立解得:y1=
| 1 |
| 2 |
代入②得:t2=8
依题意直线AB的斜率大于0,即t>0,
∴t=2
| 2 |
故直线AB的方程为x-2
| 2 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了分析推理和基本的运算能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
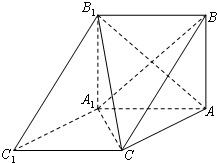 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2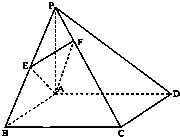 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,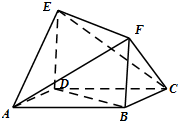 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,
 已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.
已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.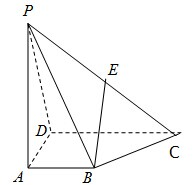 如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.
如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.