题目内容
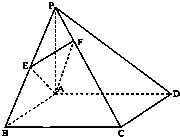 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,BC=
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,BC=| 2 |
| 1 |
| 4 |
(1)求证:AE⊥PC;
(2)求证:平面AEF⊥平面PCD.
考点:平面与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)先根据线面垂直的判定定理证明出BC⊥平面PAB,进而根据线面垂直的性质推断出AE⊥BC,然后根据线面垂直的判定定理证明出AE⊥平面PBC,则AE⊥PC得证;
(2)证明△PFA∽△PAC,可得∠PFA=∠PAC=90°,PC⊥AF,利用AE⊥PC,可以证明PC⊥平面AEF,即可证明平面AEF⊥平面PCD.
(2)证明△PFA∽△PAC,可得∠PFA=∠PAC=90°,PC⊥AF,利用AE⊥PC,可以证明PC⊥平面AEF,即可证明平面AEF⊥平面PCD.
解答:
证明:(1)∵AP=AB,E是PB的中点,
∴AE⊥PB,
∵PA⊥平面ABCD,
∴PA⊥BC,
∵AB⊥BC且PA∩AB=A,
∴BC⊥平面PAB,
∵AE?平面PAB,
∴AE⊥BC,
∵PB∩BC=B,
∴AE⊥平面PBC,
∴AE⊥PC;
(2)设PA=a,则AC=
a,∴PC=2a,
∵PF=
PC,∴PF=
,
∴△PFA∽△PAC,
∴∠PFA=∠PAC=90°,
∴PC⊥AF,
∵AE∩AF=A,
∴PC⊥平面AEF,
∵PC?平面PCD,
∴平面AEF⊥平面PCD.
∴AE⊥PB,
∵PA⊥平面ABCD,
∴PA⊥BC,
∵AB⊥BC且PA∩AB=A,
∴BC⊥平面PAB,
∵AE?平面PAB,
∴AE⊥BC,
∵PB∩BC=B,
∴AE⊥平面PBC,
∴AE⊥PC;
(2)设PA=a,则AC=
| 3 |
∵PF=
| 1 |
| 4 |
| a |
| 2 |
∴△PFA∽△PAC,
∴∠PFA=∠PAC=90°,
∴PC⊥AF,
∵AE∩AF=A,
∴PC⊥平面AEF,
∵PC?平面PCD,
∴平面AEF⊥平面PCD.
点评:本题主要考查了线面垂直和面面垂直的判定定理的应用.考查了学生空间观察能力和推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
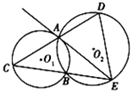 已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.
已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.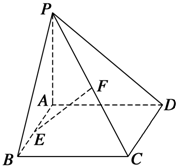 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证:
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证: 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AB=2
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AB=2