题目内容
关于下列说法：
①空集是任意集合的真子集；
②由f（x）=cos（2x-
）的图象向左平移
个单位可以得到y=cos2x的图象；
③已知函数y=ax+1-2（a＞0，且a≠1）的图象恒过定点（-1，-1）；
④非零向量
、
，若向量
在
方向上的投影与
在
方向上的投影相等，则|
|=|
|；
正确命题的序号是 （填上你认为正确命题的序号）．
①空集是任意集合的真子集；
②由f（x）=cos（2x-
| π |
| 3 |
| π |
| 6 |
③已知函数y=ax+1-2（a＞0，且a≠1）的图象恒过定点（-1，-1）；
④非零向量
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
正确命题的序号是
考点：命题的真假判断与应用
专题：简易逻辑
分析：①空集不是本身的真子集，可知不正确；
②由f（x）=cos（2x-
）的图象向左平移
个单位可以得到y=cos[2(x+
)-
]=cos2x，即可判断出；
③当x=-1时，函数y=ax+1-2=a0-2=-1，因此函数的图象恒过定点（-1，-1）；
④非零向量
、
，若
⊥
，则向量
在
方向上的投影与
在
方向上的投影相等都为0，而|
|=|
|不一定成立．
②由f（x）=cos（2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
③当x=-1时，函数y=ax+1-2=a0-2=-1，因此函数的图象恒过定点（-1，-1）；
④非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
解答：
解：①空集不是本身的真子集，不正确；
②由f（x）=cos（2x-
）的图象向左平移
个单位可以得到y=cos[2(x+
)-
]=cos2x，因此正确；
③当x=-1时，函数y=ax+1-2=a0-2=-1，因此函数的图象恒过定点（-1，-1），正确；
④非零向量
、
，若
⊥
，则向量
在
方向上的投影与
在
方向上的投影相等都为0，则|
|=|
|不一定成立，因此不正确．
综上可得：正确命题的序号是②③．
故答案为：②③．
②由f（x）=cos（2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
③当x=-1时，函数y=ax+1-2=a0-2=-1，因此函数的图象恒过定点（-1，-1），正确；
④非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
综上可得：正确命题的序号是②③．
故答案为：②③．
点评：本题考查了集合的有关性质、三角函数变换、指数函数性质、向量的投影意义、命题真假的判定，考查了推理能力吗，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
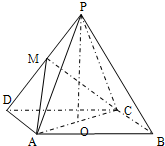如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC，O为AC中点，PO⊥平面ABCD，M为PD中点．若AC=2PO，求二面角P-AB-C的正切值．