题目内容
 如图,正方体的棱长为a且正方体各面的中心是一个几何体的顶点,求这个几何体的棱长.
如图,正方体的棱长为a且正方体各面的中心是一个几何体的顶点,求这个几何体的棱长.考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:建立空间直角坐标系,利用向量法能求出这个几何体的棱长.
解答:
 解:如图,建立空间直角坐标系,
解:如图,建立空间直角坐标系,
∵正方体的棱长为a,
∴E(
,
,a),F(
,
,0),M(
,a,
),
N(0,
,
),P(
,0,
),Q(a,
,
).
这个几何体是正八面体,
棱长|PQ|=
=
a.
∴这个几何体的棱长为
a.
 解:如图,建立空间直角坐标系,
解:如图,建立空间直角坐标系,∵正方体的棱长为a,
∴E(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
N(0,
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
这个几何体是正八面体,
棱长|PQ|=
(
|
=
| ||
| 2 |
∴这个几何体的棱长为
| ||
| 2 |
点评:本题考查几何体的棱长的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
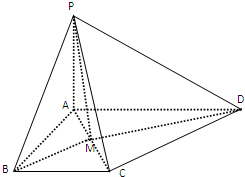 如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.
如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.