题目内容
某盒子里装有大小、形状完全相同的卡片10张,上面分别写着数字0,1,2,3,以下是10张卡片上的数字的统计结果:
根据表中信息解答以下问题:
(Ⅰ)从10张卡片中随机抽取2张,求这两张卡片上的数字之和为4的概率;
(Ⅱ)从10张卡片中随机抽取2张,用X表示抽取的这两张卡片上的数字之差的绝对值,求随机变量X的分布列及数字期望.
| 数字 | 0 | 1 | 2 | 3 |
| 卡片张数 | 1 | 2 | 3 | 4 |
(Ⅰ)从10张卡片中随机抽取2张,求这两张卡片上的数字之和为4的概率;
(Ⅱ)从10张卡片中随机抽取2张,用X表示抽取的这两张卡片上的数字之差的绝对值,求随机变量X的分布列及数字期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(Ⅰ)两张卡片上的数字之和为4,包括2+2与1+3两种情况,可得结论.
(Ⅱ)由已知得,X=0,1,2,3,注意到各事件之间的独立性与互斥性,根据相互独立事件同时发生的概率写出概率,即可求出X的分布列和数学期望.
(Ⅱ)由已知得,X=0,1,2,3,注意到各事件之间的独立性与互斥性,根据相互独立事件同时发生的概率写出概率,即可求出X的分布列和数学期望.
解答:
解:(Ⅰ)记事件A:两张卡片上的数字之和为4,则P(A)=
=
;
(Ⅱ)X=0,1,2,3,则
P(X=0)=
=
,P(X=1)=
=
,
P(X=2)=
=
,P(X=3)=
=
,
X的分布列为
EX=0×
+1×
+2×
+3×
=
.
| ||||||
|
| 11 |
| 45 |
(Ⅱ)X=0,1,2,3,则
P(X=0)=
| ||||||
|
| 2 |
| 9 |
| ||||||||||
|
| 4 |
| 9 |
P(X=2)=
| ||||||
|
| 11 |
| 45 |
| ||
|
| 4 |
| 45 |
X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 2 |
| 9 |
| 4 |
| 9 |
| 11 |
| 45 |
| 4 |
| 45 |
| 6 |
| 5 |
点评:本题考查离散型随机变量的分布列及期望,考查古典概型概率计算公式,考查学生对问题的阅读理解能力.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
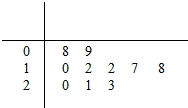 现从某100件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,
现从某100件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,