题目内容
20.已知函数f(x)=$\frac{2x}{{{x^2}+1}}$,则下列说法正确的是( )| A. | 函数f(x)在(0,+∞)上有最小值 | B. | 函数f(x)在(0,+∞)上没有最大值 | ||
| C. | 函数f(x)在R上没有极小值 | D. | 函数f(x)在R上有极大值 |
分析 求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:f′(x)=$\frac{-{2x}^{2}+2}{{{(x}^{2}+1)}^{2}}$,
令f′(x)>0,解得:-1<x<1,
令f′(x)<0,解得:x>1或x<-1,
故f(x)在(-∞,-1)递减,在(-1,1)递增,在(1,+∞)递减,
故f(x)在R有极大值,
故选:D.
点评 本题考查了函数的单调性、极值、最值问题,是一道基础题.

练习册系列答案
相关题目
11.下列结论中,正确的是( )
| A. | “x>2”是“x2-2x>0”成立的必要条件 | |
| B. | 命题“若x2=1,则x=1”的逆否命题为假命题 | |
| C. | 命题“p:?x∈R,x2≥0”的否定形式为“¬p:?x0∈R,x02≥0” | |
| D. | .已知向量$\overrightarrow a,\overrightarrow b$,则“$\overrightarrow a∥\overrightarrow b$”是“$\overrightarrow a+\overrightarrow b=\overrightarrow 0$”的充要条件 |
15.在四边形 ABCD 中,若$\overrightarrow{AB}$=-$\frac{1}{2}$$\overrightarrow{CD}$,则此四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 梯形 | D. | 矩形 |
 四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.
四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.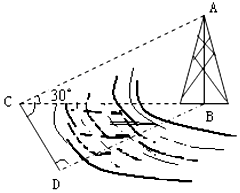 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.