题目内容
18.已知曲线C1:$\left\{\begin{array}{l}{x=1+t}\\{y=-3-\frac{3}{4}t}\end{array}\right.$(t为参数)与曲线C2:ρ2-4ρ•cosθ-21=0交于A,B两点,求线段AB的长,并说明C1,C2分别是什么曲线?分析 曲线C1:$\left\{\begin{array}{l}{x=1+t}\\{y=-3-\frac{3}{4}t}\end{array}\right.$(t为参数),把t=x-1代入y=-3-$\frac{3}{4}$t,可得普通方程.曲线C2:ρ2-4ρ•cosθ-21=0,利用互化公式可得:直角坐标方程.求出圆心曲线C2到直线的距离d,可得|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:曲线C1:$\left\{\begin{array}{l}{x=1+t}\\{y=-3-\frac{3}{4}t}\end{array}\right.$(t为参数),把t=x-1代入y=-3-$\frac{3}{4}$t,可得y=-3-$\frac{3}{4}$(x-1),化为:3x+4y+9=0,因此曲线C1表示直线.
曲线C2:ρ2-4ρ•cosθ-21=0,利用互化公式可得:x2+y2-4x-21=0,配方为(x-2)2+y2=25,曲线C2表示圆心为C2(2,0),半径为r=5.
圆心曲线C2到直线的距离d=$\frac{|2×3+0+9|}{\sqrt{{3}^{2}+{4}^{2}}}$=3,
∴|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=2×$\sqrt{{5}^{2}-{3}^{2}}$=8.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式、直线与圆相交弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.命题“?x∈R,x2-2x+1<0”的否定是( )
| A. | ?x∈R,x2-2x+1≥0 | B. | ?x∈R,x2-2x+1>0 | C. | ?x∈R,x2-2x+1≥0 | D. | ?x∈R,x2-2x+1<0 |
13.命题“任意x∈R,|x|+x2≥0”的否定是( )
| A. | 任意x∈R,|x|+x2<0 | B. | 存在x∈R,|x|+x2≤0 | ||
| C. | 存在x0∈R,|x0|+x02<0 | D. | 存在x0∈R,|x0|+x02≥0 |
3.若函数y=f(2x)的定义域是[1,2],则函数f(log2x)的定义域是( )
| A. | [1,2] | B. | [4,16] | C. | [0,1] | D. | [2,4] |
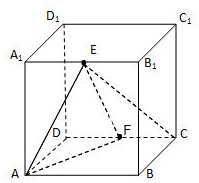 在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.