题目内容

15．设{an}是公差为d（d≠0）的等差数列，它的前10项和S10=110且a1，a2，a4成等比数列，求数列{an}的通项公式及其前n项和．

分析 通过2a1+9d=22与a22=a1a4，进而计算即可求出数列{an}的通项公式，再根据前n项和公式计算可得．

解答 解：设{an}的前n项和为Sn，
∵S10=110，
∴2a1+9d=22．    …①
∵a1，a2，a4成等比数列，
∴a22=a1a4． …②
由①、②，解得：a1=d=2，
∴an=2n；
∴Sn=$\frac{n（2n+2）}{2}$=n（n+1）

点评 本题考查数列的通项及前n项和，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
5．已知一组数据3，5，4，7，6，那么这组数据的方差为2．
6．命题“?x∈R，x2-2x+1＜0”的否定是（　　）
A．?x∈R，x2-2x+1≥0B．?x∈R，x2-2x+1＞0C．?x∈R，x2-2x+1≥0D．?x∈R，x2-2x+1＜0
3．若函数y=f（2x）的定义域是[1，2]，则函数f（log2x）的定义域是（　　）
A．[1，2]B．[4，16]C．[0，1]D．[2，4]
10．已知等比数列{an}的前n项和为Sn，且S6=S3+14，a6=10-a4，a4＞a3．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）数列{bn}中，bn=log2 an，求数列{an•bn }的前n项和Tn．
20．设集合M={x|$\frac{x+3}{5-x}$＞0}，N={x|log3x≥1}，则M∩N=（　　）
A．[3，5）B．[1，3]C．（5，+∞）D．（-3，3]
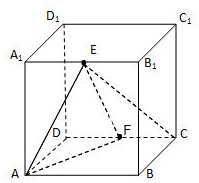7．在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别为A1B1，CD的中点．
（1）求直线EC与平面B1BCC1所成角的大小的正弦值；
（2）求二面角E-AF-B的余弦值．
4．设函数f（x）=|x-a|-2|x-1|．
（Ⅰ）当a=3时，解不等式f（x）≥1；
（Ⅱ）若f（x）-|2x-5|≤0对任意的x∈[1，2]恒成立，求实数a的取值范围．
5．已知椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$的左、右焦点分别为F1，F2，过左焦点F1的直线交椭圆于A，B两点，则△ABF2的周长为（　　）
A．12B．9C．6D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网