题目内容
已知函数f(x)=x2+2x.
(Ⅰ)若f(x)在[-3,a]上单调递减,求实数a的取值范围;
(Ⅱ)若存在实数t,当x∈[1,m],f(x+t)≤3x恒成立,求实数m的取值范围.
(Ⅰ)若f(x)在[-3,a]上单调递减,求实数a的取值范围;
(Ⅱ)若存在实数t,当x∈[1,m],f(x+t)≤3x恒成立,求实数m的取值范围.
考点:二次函数在闭区间上的最值,函数单调性的判断与证明
专题:
分析:(Ⅰ)根据f(x)=(x+1)2-1 在[-3,a]上单调递减,利用二次函数的性质求得a的范围.
(Ⅱ)由题意可得 x∈[1,m]时,x2+(2t-1)x+t2+2t≤0恒成立.令u(x)=x2+(2t-1)x+t2+2t,则
.令g(t)=t2+2(m+1)t+m2-m,问题转化为当t∈[-4,0],g(t)的最大值为非正实数.分类讨论,求得m的范围.
(Ⅱ)由题意可得 x∈[1,m]时,x2+(2t-1)x+t2+2t≤0恒成立.令u(x)=x2+(2t-1)x+t2+2t,则
|
解答:
解:(Ⅰ)∵f(x)=x2+2x=(x+1)2-1 在[-3,a]上单调递减,
∴-3<a≤-1.
(Ⅱ)若存在实数t,当x∈[1,m],f(x+t)≤3x恒成立,
则 x∈[1,m]时,x2+(2t-1)x+t2+2t≤0恒成立.
令u(x)=x2+(2t-1)x+t2+2t,则
,即
.
令g(t)=t2+2(m+1)t+m2-m,问题转化为存在t∈[-4,0],使得g(t)≤0 成立,
即 当t∈[-4,0],g(t)的最大值为非正实数.
由于函数g(t)的对称轴为t=-1-m<-2,
①当-1-m<-4,即 m>3时,g(t)min=g(-4)=16-8(m+1)+m2-m≤0,
求得 3<m≤8.
②当-4≤-1-m≤-2,即 1<m≤3时,g(t)min=g(-1-m)=-1-3m≤0,
求得 1<m≤3.
综上可得,m的范围为(1,8].
∴-3<a≤-1.
(Ⅱ)若存在实数t,当x∈[1,m],f(x+t)≤3x恒成立,
则 x∈[1,m]时,x2+(2t-1)x+t2+2t≤0恒成立.
令u(x)=x2+(2t-1)x+t2+2t,则
|
|
令g(t)=t2+2(m+1)t+m2-m,问题转化为存在t∈[-4,0],使得g(t)≤0 成立,
即 当t∈[-4,0],g(t)的最大值为非正实数.
由于函数g(t)的对称轴为t=-1-m<-2,
①当-1-m<-4,即 m>3时,g(t)min=g(-4)=16-8(m+1)+m2-m≤0,
求得 3<m≤8.
②当-4≤-1-m≤-2,即 1<m≤3时,g(t)min=g(-1-m)=-1-3m≤0,
求得 1<m≤3.
综上可得,m的范围为(1,8].
点评:本题主要考查二次函数的性质,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,已知a=
,b=
,B=45°,则角A为( )
| 3 |
| 2 |
| A、60° |
| B、150° |
| C、60°或 150° |
| D、60°或120° |
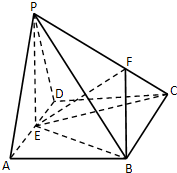 如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=
如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=