题目内容
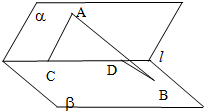如图，已知二面角α-l-β为60°，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，且AC=2，CD=3，DB=1，则AB的长度为（ ）| A、4 | ||||
B、2
| ||||
C、3
| ||||
D、
|
考点：与二面角有关的立体几何综合题
专题：计算题,空间位置关系与距离
分析：求出线段AB表示的向量与AC、CD，DB，对应的向量的关系，利用向量的数量积求解即可．
解答：
解：∵
=
+
+
，
∴
2=（
+
+
）2=
+
+
+2
•
+2
•
+2
•
=4+9+1+2•2•1•cos120°=12
∴AB的长度为2
．
故选：B．
| AB |
| AC |
| CD |
| DB |
∴
| AB |
| AC |
| CD |
| DB |
| AC |
| CD |
| DB |
| AC |
| CD |
| AC |
| DB |
| CD |
| DB |
∴AB的长度为2
| 3 |
故选：B．
点评：本题考查空间两点间的距离的求法，考查数量积的应用，基本知识的考查．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
已知x，y都是正数，且xy=1，则x+y的最小值为（ ）
| A、4 | B、3 | C、2 | D、1 |
下列命题正确的是（ ）
| A、ac＜bc⇒a＜b | ||||
B、若a＜b＜0，则，
| ||||
C、当x＞0且x≠1时，lgx+
| ||||
D、
|
圆x2+y2=1的圆心到直线x-y+2=0的距离为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
已知椭圆
+y2=1，椭圆的中心为坐标原点O，点F是椭圆的右焦点，点A是椭圆短轴的一个端点，过点F的直线l与椭圆交于M、N两点，与OA所在直线交于E点，若
=λ1
，
=λ2
，则λ1+λ2=（ ）
| x2 |
| 5 |
| EM |
| MF |
| EN |
| NF |
| A、-10 | B、10 | C、-5 | D、5 |
一元二次不等式x2-x-2＞0的解集是（ ）
| A、（∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-∞，-2）∪（1，+∞） |
| D、（-2，1） |
不等式x2＞2x的解集为（ ）
| A、{x|x＞2} |
| B、{x|x＜0} |
| C、{x|0＜x＜2} |
| D、{x|x＜0，或x＞2} |