题目内容
17.已知椭圆x2+4y2=1的长轴长为( )| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
分析 根据题意,将椭圆的方程变形为标准方程,分析可得a的值,进而由长轴的定义可得答案.
解答 解:根据题意,椭圆的方程为:x2+4y2=1,
化为标准方程可得:$\frac{{x}^{2}}{1}$+$\frac{{y}^{2}}{\frac{1}{4}}$=1,
其中a=$\sqrt{1}$=1,
则其长轴长2a=2;
故选:C.
点评 本题考查椭圆的标准方程,注意要先将其方程化为标准方程.

练习册系列答案
相关题目
8.在△ABC中,A=30°,则$\sqrt{3}sinA-cos({B+C})$的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
12.复数(1-i)•(1+i)的值是( )
| A. | -2i | B. | 2i | C. | 2 | D. | -2 |
7.已知点P是以F1,F2为焦点的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$上一点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0,tan∠P{F_1}{F_2}=\frac{1}{3}$,则椭圆的离心率是( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
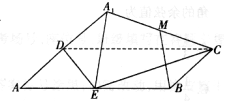 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中: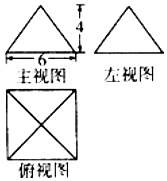 已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.