题目内容
P是边长为a的正六边形ABCDEF所在平面外α的一点，且PA⊥α，PA=a，则P点到直线CD的距离为 ．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：由已知中P是边长为a的正六边形ABCDEF所成平面外一点，PA⊥AB，PA⊥AF，PA=a．我们易得PA⊥平面ABCDEF，解直角三角形PAC，PAD后，可由勾股定理判断出PC⊥CD，即可得到答案．
解答：
解：连接AC，AD，PD，如下图所示：
∵正六边形ABCDEF的边长为a，则AC=
a，AD=2a，CD=a
PA⊥α，PA=a，
∴PA⊥AC，PA⊥AD．
则PC=2a，PD=
a，
在△PCD中，∵PC2+CD2=PD2，
故PC⊥CD
故PC长即为P点到CD的距离
故答案为：2a．
解：连接AC，AD，PD，如下图所示：∵正六边形ABCDEF的边长为a，则AC=
| 3 |
PA⊥α，PA=a，
∴PA⊥AC，PA⊥AD．
则PC=2a，PD=
| 5 |
在△PCD中，∵PC2+CD2=PD2，
故PC⊥CD
故PC长即为P点到CD的距离
故答案为：2a．
点评：本题考查的知识点是空间点到线之间的距离，其中证明PC⊥CD，进而将点到直线的距离，转化为求线段长问题，是解答本题的关键．
练习册系列答案
相关题目
设集合U=R，A={x∈N|x≤3}，B={-2，-1，0，1，2}，则（∁UA）∩B等于（ ）
| A、{-2，-1，0} |
| B、{-2，-1} |
| C、{1，2} |
| D、{0，1，2} |
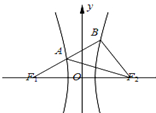如图，F1，F2是双曲线C：