题目内容
 下列命题中:
下列命题中:①某中学高三(1)班有学生m人,现按座位号的编号采用系统抽样的方法选取5名同学参加一项活动,已知座位号为5号、16号、27号、38号、49号的同学均被选出,则该班的学生人数m的取值范围为[55,59];
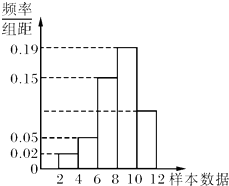
②有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为20;
③已知圆C:x2+y2=12,直线l:4x+3y=25.圆C上任意一点A到直线l的距离小于2的概率为
| 1 |
| 6 |
④已知回归直线y=bx+a的回归系数b的估计值是1.23,
. |
| y |
. |
| x |
正确命题的序号为:
考点:频率分布直方图,线性回归方程
专题:概率与统计
分析:①由系统抽样方法知,将总体分成均衡的若干部分,分段的间隔要求相等,间隔一般为总体的个数除以样本容量,据此可得答案;
②根据频率分布直方图求出样本数据落在区间[10,12)内的频率与频数;
③画出图形,结合图形求出圆心到直线l的距离以及半径r,从而得出圆C上任意一点A到直线l的距离小于2的圆弧,即可求出概率;
④由回归直线y=bx+a过样本的中心点(
,
),从而求得回归直线方程.
②根据频率分布直方图求出样本数据落在区间[10,12)内的频率与频数;
③画出图形,结合图形求出圆心到直线l的距离以及半径r,从而得出圆C上任意一点A到直线l的距离小于2的圆弧,即可求出概率;
④由回归直线y=bx+a过样本的中心点(
. |
| x |
. |
| y |
解答:
解:对于①,按系统抽样的方法,是将总体分成均衡的5部分,分段的间隔是11,∴总体个数m满足:11×5≤m<12×5,即55≤m<60,①正确;
对于②,根据频率分布直方图得,样本数据落在区间[10,12)内的频率为:1-(0.02+0.05+0.15+0.19)×2=0.18
∴频数为200×0.18=36;∴②错误;
对于③,圆心(0,0)到直线l的距离d=
=5,半径r=2
,如图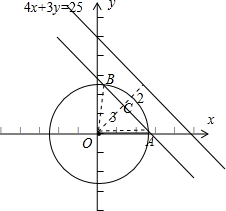 ;
;
∵OC=5-2=3,∴OA=OB=2
,∴cos∠AOC=
=
,
∴∠AOC=
,∴∠AOB=2∠AOC=
;∴
上的点到直线l的距离小于2,即圆C上任意一点A到直线l的距离小于2的概率为
;∴③正确;
对于④,由回归直线y=bx+a,求得a=
-b
=5-1.23×4=0.08,∴回归直线方程是y=1.23x+0.08,∴④正确.
∴以上正确的命题是①③④.
故故答案为:①③④.
对于②,根据频率分布直方图得,样本数据落在区间[10,12)内的频率为:1-(0.02+0.05+0.15+0.19)×2=0.18
∴频数为200×0.18=36;∴②错误;
对于③,圆心(0,0)到直线l的距离d=
| 25 |
| 5 |
| 3 |
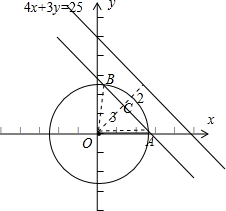 ;
;∵OC=5-2=3,∴OA=OB=2
| 3 |
| 3 | ||
2
|
| ||
| 2 |
∴∠AOC=
| π |
| 6 |
| π |
| 3 |
 |
| AB |
| 1 |
| 6 |
对于④,由回归直线y=bx+a,求得a=
. |
| y |
. |
| x |
∴以上正确的命题是①③④.
故故答案为:①③④.
点评:本题考查了频率分布直方图以及概率的有关知识应用问题,解题时应对每一个选项认真分析,从而选出正确的答案.

练习册系列答案
相关题目
在△ABC中,已知cos
=
,则cos
=( )
| A+B |
| 2 |
| 1 |
| 5 |
| C |
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
下列函数中,既是偶函数,又在区间[-1,0]上是减函数的是( )
| A、y=cosx |
| B、y=x2 |
| C、y=log2x |
| D、y=ex-e-x |