题目内容
已知圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,且A,B两点恰好将此双曲线的焦距三等分,则此双曲线的标准方程为 .
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出A(0,-3),B(0,3),从而得到a=3,2c=18,由此能求出双曲线方程.
解答:
解:解方程组
,得
或
,
∵圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,
且A,B两点恰好将此双曲线的焦距三等分,
∴A(0,-3),B(0,3),
∴a=3,2c=18,∴b2=(
)2-32=72,
∴双曲线方程为
-
=1.
故答案为:为
-
=1.
|
|
|
∵圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,
且A,B两点恰好将此双曲线的焦距三等分,
∴A(0,-3),B(0,3),
∴a=3,2c=18,∴b2=(
| 18 |
| 2 |
∴双曲线方程为
| y2 |
| 9 |
| x2 |
| 72 |
故答案为:为
| y2 |
| 9 |
| x2 |
| 72 |
点评:本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,要熟练掌握双曲线的简单性质.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
要得到函数y=tan(2x+
)的图象,只须将y=tan2x的图象上的所有的点( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
如图:若输出结果在区间[-2,2]内,则输入x的取值范围是( )

| A、[-2,0] |
| B、[-3,-1] |
| C、[-2,1] |
| D、[-1,3] |
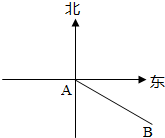 已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.
已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.
 下列命题中:
下列命题中: