题目内容
已知在△ABC中,角A、B、C所对的边分别为a、b、c,b(b-
c)=(a-c)(a+c),且角B为钝角.
(1)求角A的大小;
(2)若a=
,求b-
c的取值范围.
| 3 |
(1)求角A的大小;
(2)若a=
| 1 |
| 2 |
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)由条件利用余弦定理求得cosA=
的值,可得A的值.
(2)由正弦定理可得b-
c=-sin(B+
),根据角B为钝角,且B<π-A,可得B+
的范围,再根据正弦函数的定义域和值域,求得b-
c的取值范围.
| b2+c2-a2 |
| 2bc |
(2)由正弦定理可得b-
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
解答:
解:(1)在△ABC中,由b(b-
c)=(a-c)(a+c),可得b2+c2-a2=
bc,
故由余弦定理可得cosA=
=
,∴A=
.
且角B为钝角.
(2)∵a=
,A=
,由正弦定理可得
=2r,即2r=
=1(r为三角形外接圆的半径),且 B+C=
.
故b-
c=sinB-
sinC=sinB-
sin(
-B)=sinB-
(sin
cosB-cos
sinB)
=-
sinB-
cosB=-sin(B+
),
根据角B为钝角,且B<π-A=
,可得B+
∈(
,
),
故sin(B+
)∈(-
,
),故-sin(B+
)∈(-
,
),
即b-
c的取值范围为(-
,
).
| 3 |
| 3 |
故由余弦定理可得cosA=
| b2+c2-a2 |
| 2bc |
| ||
| 2 |
| π |
| 6 |
且角B为钝角.
(2)∵a=
| 1 |
| 2 |
| π |
| 6 |
| a |
| sinA |
| ||
sin
|
| 5π |
| 6 |
故b-
| 3 |
| 3 |
| 3 |
| 5π |
| 6 |
| 3 |
| 5π |
| 6 |
| 5π |
| 6 |
=-
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
根据角B为钝角,且B<π-A=
| 5π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
| 7π |
| 6 |
故sin(B+
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
即b-
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查正弦定理和余弦定理的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
函数f(x)的部分图象如图所示,则f(x)的解析式为( )
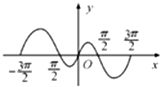

| A、f(x)=x+sinx | ||||
B、f(x)=
| ||||
| C、f(x)=xcosx | ||||
D、f(x)=x(x-
|
 设非零向量向量
设非零向量向量 已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证:
已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证: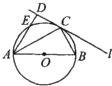 如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为
如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为