题目内容
17．如图是一个算法的流程图，最后输出的S=127
分析 按照程序框图的流程写出每一次循环的结果，并判断每一次得到的结果是否满足判断框中的条件，直到满足条件，退出循环，执行输出．
解答 解：模拟执行程序，可得
S=0，i=1
执行循环体，S=1，i=2
不满足条件S＞100，执行循环体，S=3，i=3
不满足条件S＞100，执行循环体，S=7，i=4
不满足条件S＞100，执行循环体，S=15，i=5
不满足条件S＞100，执行循环体，S=31，i=6
不满足条件S＞100，执行循环体，S=63，i=7
不满足条件S＞100，执行循环体，S=127，i=8
满足条件S＞100，退出循环，输出S的值为127．
故答案为：127．
点评 本题考查解决程序框图中的循环结构时；常采用写出前几次循环的结果，找规律，属于基础题．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
7．若直线y=2x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1没有公共点，则双曲线的离心率的取值范围是（ ）
| A． | [$\sqrt{3}$，+∞） | B． | [$\sqrt{5}$，+∞） | C． | （1，$\sqrt{3}$] | D． | （1，$\sqrt{5}$] |
5．在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0\;，\;b＞0\;，\;c=\sqrt{{a^2}+{b^2}}}）$中，已知c，a，b成等差数列，则该双曲线的离心率等于（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{{\sqrt{3}+1}}{2}$ | C． | $\frac{5}{4}$ | D． | $\frac{{\sqrt{5}+1}}{2}$ |
12．“p∨q为真”是“￢p为假”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
2．不等式x（x-5）2＞3（x-5）2的解集是（ ）
| A． | {x|x＜-3} | B． | {x|3＜x＜5或x＞5} | C． | {x|x＞5} | D． | {x|3＜x＜5} |
9．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，其一条渐近线为x+$\sqrt{2}$y=0，点M在双曲线上，且MF1⊥x轴，若F2同时为抛物线y2=12x的焦点，则F1到直线F2M的距离为（ ）
| A． | $\frac{{3\sqrt{6}}}{5}$ | B． | $\frac{{5\sqrt{6}}}{6}$ | C． | $\frac{5}{6}$ | D． | $\frac{6}{5}$ |
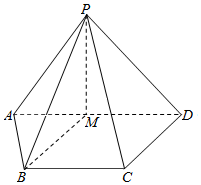如图，在四棱锥P-ABCD中，AD∥BC，且AD=2BC，AD⊥CD，PA=PD，M为棱AD的中点．