题目内容
19.若函数$y=sin({2x+φ})({0<φ<\frac{π}{2}})$的图象的对称中心在区间$({\frac{π}{6},\frac{π}{3}})$内有且只有一个,则φ的值可以是( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
分析 根据正弦函数图象的对称中心是(kπ,0),求出φ的表达式,再根据题意求出φ的取值范围,即可得出φ的一个可能取值.
解答 解:根据题意,令2x+φ=kπ,k∈Z,
得φ=kπ-2x,k∈Z;
又函数f(x)图象的对称中心在区间($\frac{π}{6}$,$\frac{π}{3}$)内,
∴-2x∈(-$\frac{2π}{3}$,-$\frac{π}{3}$),
∴kπ-2x∈(kπ-$\frac{2π}{3}$,kπ-$\frac{π}{3}$),k∈Z;
当k=1时,φ∈($\frac{π}{3}$,$\frac{2π}{3}$),
又0<φ<$\frac{π}{2}$,
∴φ的一个可能取值是$\frac{5π}{12}$.
故选:D.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
10.下列命题正确的是( )
| A. | ?x0∈R,sinx0+cosx0=$\frac{3}{2}$ | |
| B. | ?x≥0且x∈R,2x>x2 | |
| C. | 已知a,b为实数,则a>2,b>2是ab>4的充分条件 | |
| D. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 |
14.欧拉(Leonhard Euler,国籍瑞士)是科学史上最多产的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式可知,表示的复数e-iπ在复平面内位于
( )
( )
| A. | 第一象限 | B. | 在实数轴上 | C. | 第三象限 | D. | 第四象限 |
9.已知x,y满足$\left\{\begin{array}{l}{x-1≤0}\\{y-2≤0}\\{2x+y-2>0}\end{array}\right.$若$\overrightarrow{m}$=(x+1,y)则$\sqrt{{\overrightarrow{m}}^{2}}$的取值范围为( )
| A. | (15,2) | B. | ($\frac{29}{2}$,2$\sqrt{2}$) | C. | (17,2$\sqrt{2}$) | D. | ($\frac{4\sqrt{5}}{5}$,2$\sqrt{2}$] |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,AB=1,$∠ABC=\frac{π}{3}$,E为PD中点,PA=1.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,AB=1,$∠ABC=\frac{π}{3}$,E为PD中点,PA=1.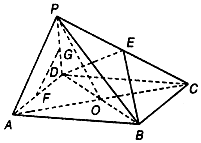 如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC、BD相交于点O,点E、F、G分别为PC、AD、PD的中点,OP=OA,PA⊥PD.
如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC、BD相交于点O,点E、F、G分别为PC、AD、PD的中点,OP=OA,PA⊥PD.