题目内容
7. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,AB=1,$∠ABC=\frac{π}{3}$,E为PD中点,PA=1.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,AB=1,$∠ABC=\frac{π}{3}$,E为PD中点,PA=1.(I)求证:PB∥平面AEC;
(Ⅱ)在棱PC上是否存在点M,使得直线PC⊥平面BMD?若存在,求出点M的位置;若不存在,说明理由.
分析 (I)连接BD,交AC于点O,连接EO,由ABCD为菱形,可得:O为BD中点,利用中位线的性质可证EO∥PB,利用线面平行的判定即可证明PB∥平面AEC;
(Ⅱ)若在棱PC上存在点M,使得直线PC⊥平面BMD,只需PC⊥BM即可.若PC⊥BM,由于PC⊥BO,可得PC⊥OM,由△COM∽△PAC,可得$\frac{CM}{AC}=\frac{CO}{PC}$,根据已知可求CM的值,即可得解.
解答 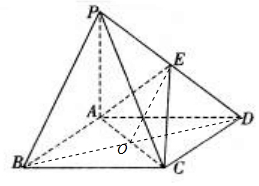 解:(I)证明:如图,连接BD,交AC于点O,连接EO,
解:(I)证明:如图,连接BD,交AC于点O,连接EO,
∵ABCD为菱形,可得:O为BD中点,
又∵E为PD中点,
∴EO∥PB,
∵EO?平面AEC,PB?平面AEC,
∴PB∥平面AEC;
解:(Ⅱ)在棱PC上存在点M,当CM=$\frac{\sqrt{2}}{4}$时,使得直线PC⊥平面BMD,理由如下:
∵PA⊥平面ABCD,BD?平面ABCD,
∴BD⊥PA,
又∵ABCD为菱形,
∴BD⊥AC,
∴由PA∩AC=A,可得:BD⊥平面PAC,
∴由PC?平面PAC,可得:BD⊥PC,
∴若在棱PC上存在点M,使得直线PC⊥平面BMD,只需PC⊥BM即可.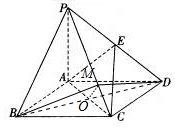
∵若PC⊥BM,由于PC⊥BO,
∴PC⊥平面BOM,可得PC⊥OM,
∴△COM∽△PAC,可得:$\frac{CM}{AC}=\frac{CO}{PC}$,可得:$\frac{CM}{1}=\frac{\frac{1}{2}}{\sqrt{2}}$,解得:CM=$\frac{\sqrt{2}}{4}$,
∴在棱PC上存在点M,当CM=$\frac{\sqrt{2}}{4}$时,使得直线PC⊥平面BMD.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.设复数z满足(1-i)z=3+i,则z=( )
| A. | 1+2i | B. | 2+2i | C. | 2-i | D. | 1+i |
19.若函数$y=sin({2x+φ})({0<φ<\frac{π}{2}})$的图象的对称中心在区间$({\frac{π}{6},\frac{π}{3}})$内有且只有一个,则φ的值可以是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
16.已知圆C:(x-$\sqrt{3}$)2+(y-1)2=1和两点A(-t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )
| A. | ($\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$) | B. | ($\frac{3\sqrt{2}}{2}$,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$) | D. | ($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$) |
17.(-$\sqrt{x}$+$\frac{1}{x}$)10的展开式中x2的系数等于( )
| A. | 45 | B. | -20 | C. | -45 | D. | -90 |
 如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC=30°,PA=AB=4.
如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC=30°,PA=AB=4.