题目内容
12.设A、B是球O的球面上两点,且∠AOB=90°,若点C为该球面上的动点,三棱锥O-ABC的体积的最大值为$\frac{9\sqrt{π}}{2{π}^{2}}$立方米,则球O的表面积是36平方米.分析 当点C位于垂直于面AOB的直径端点时,三棱锥O-ABC的体积最大,由此求出球O的半径,进而能求出球O的表面积.
解答 解:如图所示,当点C位于垂直于面AOB的直径端点时,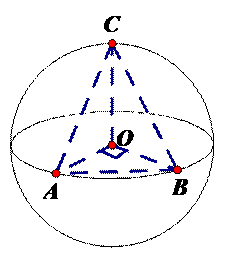
三棱锥O-ABC的体积最大,
设球O的半径为R,此时${V}_{O-ABC}={V}_{C-AOB}=\frac{1}{3}×\frac{1}{2}×{R}^{2}×R$=$\frac{9\sqrt{π}}{2{π}^{2}}$,
解得R=$\frac{3}{\sqrt{π}}$,
∴球O的表面积为S=4πR2=4π×$\frac{9}{π}$=36.
故答案为:36.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意球、三棱锥的性质及构造法的合理应用.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若m⊥α,m∥n,n∥β,则 α⊥β | B. | 若α∥β,m?α,n?β,则 m∥n | ||
| C. | 若m⊥n,m?α,n?β,则α⊥β | D. | 若α⊥β,m?α,n?β,则m⊥n |
3.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(即百分比)为“衰分比”.今共有粮38石,按甲、乙、丙的顺序进行“衰分”,已知甲分得18石,则“衰分比”为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
20.设全集U=R+,集合A={x|log0.5x≥-1},B={x||x|>1},则“x∈A”是“x∈∁UB”的( )
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.已知简单组合体的三视图如图所示,则此简单组合体的体积为( )
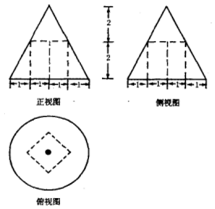

| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |
1.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,f($\frac{π}{2}$)=-1,则f(0)的值为( )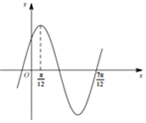

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
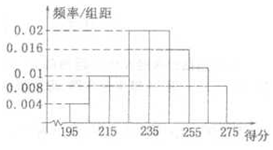 某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.
某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.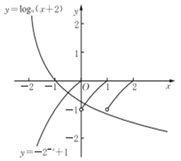 已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).
已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).