题目内容
17．化简求值：（1）$\sqrt{6\frac{1}{4}}+\sqrt{3\frac{3}{8}}+\sqrt{0.0625}{+（\sqrt{π}）}^{0}{-2}^{-1}$
（2）lg14-2lg$\frac{7}{3}$+lg7-lg18．
分析 （1）利用指数的运算法则即可得出．
（2）利用对数的运算法则即可得出．
解答 解：（1）原式=$\frac{5}{2}+\frac{3\sqrt{6}}{4}$+0.25+1-$\frac{1}{2}$=$\frac{13+3\sqrt{6}}{4}$．
（2）原式=$lg\frac{14×7}{（\frac{7}{3}）^{2}×18}$=lg1=0．
点评 本题考查了指数与对数的运算法则，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
5．依法纳税是每个公民应尽的义务，规定：公民全月工资、薪金所得不超过3500元的，免征个人所得税；超过3500元部分为全月应纳税所得额，此项税款按如表分段累计计算：
（1）若应纳税额为f（x），试用分段函数表示1～3级纳税额f（x）的计算公式；
（2）某人一月份应交纳此项税款303元，那么他当月的工资、薪金所得是多少？
| 级数 | 全月应纳税所得额x | 税率 |
| 1 | 不超过1500元部分 | 3% |
| 2 | 超过1500元至4500元部分 | 10% |
| 3 | 超过4500元至9000元部分 | 20% |
（2）某人一月份应交纳此项税款303元，那么他当月的工资、薪金所得是多少？
12．已知函数f（x）=e2x-aex+2x在R上是增函数，则实数a的取值范围是（ ）
| A． | （2，4] | B． | （-∞，4] | C． | （3，4） | D． | [3，4） |
2．设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（ ）
| A． | 若m⊥α，m∥n，n∥β，则 α⊥β | B． | 若α∥β，m?α，n?β，则 m∥n | ||
| C． | 若m⊥n，m?α，n?β，则α⊥β | D． | 若α⊥β，m?α，n?β，则m⊥n |
6．三棱柱ABC-A1B1C1的侧棱垂直于底面，且AB⊥BC，AB=BC=AA1=2，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为（ ）
| A． | 48π | B． | 32π | C． | 12π | D． | 8π |
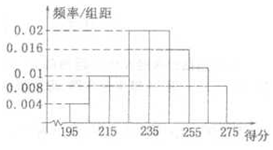某高校组织自主招生考试，共有2 000名学生报名参加了笔试，成绩均介于195分到275分 之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成八组：第一组[195，205），第二组[205，215），…，第八组[265，275]．如图是按上述分组方法得到的频率分布直方图，已知笔试成绩在260分以上（含260分）的同学取得面试资格．