题目内容
4. 正方体ABCD-A1B1C1D1被平面B1D1C截去一部分后得到几何体AB1D1-ABCD.如图所示.
正方体ABCD-A1B1C1D1被平面B1D1C截去一部分后得到几何体AB1D1-ABCD.如图所示.(1)在几何体AB1D1-ABCD的面上画出一条线段,使该线段所在的直线平行于平面B1D1C.
(2)设E为B1D1的中点,求证:B1D1⊥平面A1ECA.
分析 (1)连接BD,则BD∥平面B1D1C,利用正方形的性质及线面平行的判定定理即可证明.
(2)利用等腰三角形的性质可得B1D1⊥A1E,进而利用线面垂直的判定定理即可证明.
解答 解:(1)如图,连接BD,则BD∥平面B1D1C,
证明:∵由已知可得:BD∥B1D1,且BD?平面AB1D1,
∴BD∥平面B1D1C.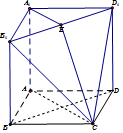
(2)证明:在等腰A1B1D1中,E为B1D1的中点,
所以,B1D1⊥A1E,
由已知可得:AA1⊥平面A1B1D1,
所以,AA1⊥B1D1,
所以,B1D1⊥平面A1ECA.
点评 本题主要考查了线面平行的判定定理,等腰三角形的性质,线面垂直的判定定理的应用,考查了数形结合思想,属于中档题.

练习册系列答案
相关题目
14.下列命题中,真命题是( )
| A. | a-b=0的充要条件是$\frac{a}{b}$=1 | B. | ?x∈R,2x>x | ||
| C. | ?x0∈R,|x0|<0 | D. | 若p∧q为假,则p∨q为假 |
12.某市有超市2000家,其中大型超市140家,中型超市400家,小型超市1460家.现采用分层抽样的方法从中抽取一个容量为100的样本,那么应抽取中型超市的数量为( )
| A. | 7 | B. | 20 | C. | 40 | D. | 73 |
19.如果函数f(x)=log3x,那么f($\frac{1}{3}$)等于( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
9.在△ABC中,角A,B,C的对边分别是a,b,c,若C=45°,c=$\sqrt{2}$a,则A等于( )
| A. | 120° | B. | 60° | C. | 150° | D. | 30° |
16.在平面直角坐标系中,与点A(1,2)的距离为2,且与直线3x-4y=0的距离为1的点共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |