题目内容
已知|
|=1,|
|=1,
与
的夹角为60°,
=2
-
,
=3
-
,则
与
的夹角的余弦值是 .
| a |
| b |
| a |
| b |
| x |
| a |
| b |
| y |
| b |
| a |
| x |
| y |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由题意易得
•
,|
|,|
|,代入夹角公式计算可得.
| x |
| y |
| x |
| y |
解答:
解:∵|
|=1,|
|=1,
与
的夹角为60°,
∴
•
=(2
-
)•(3
-
)=-2
2+7
•
-3
2
=-2×12+7×1×1×
-3×12=-
,
∴|
|=
=
=
,
|
|=
=
=
,
∴
与
的夹角的余弦值=
=-
故答案为:-
| a |
| b |
| a |
| b |
∴
| x |
| y |
| a |
| b |
| b |
| a |
| a |
| a |
| b |
| b |
=-2×12+7×1×1×
| 1 |
| 2 |
| 3 |
| 2 |
∴|
| x |
(2
|
4
|
| 3 |
|
| y |
(3
|
|
| 7 |
∴
| x |
| y |
| ||||
|
|
| ||
| 14 |
故答案为:-
| ||
| 14 |
点评:本题考查向量的夹角公式,涉及数量积和模长公式的应用,属基础题.

练习册系列答案
相关题目
若△ABC的三个内角A、B、C成等差数列,则cos(A+C)=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若集合A={x|
≤0},B={x|x≥-2}且A⊆B.则实数a的取值范围是( )
| x-a |
| x-2 |
| A、(-∞,-2] |
| B、[-2,2] |
| C、[-2,+∞) |
| D、[2,+∞) |
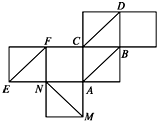 如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:
如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题: