题目内容
设数列{an}的前n项和Sn=2n+1,数列{bn}满足bn=
+n.
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn.
| 1 |
| (n+1)log2an |
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)当n=1时,a1=S1=4,n≥2时,an=Sn-Sn-1=2n+1-2n =2n,由此能求出数列{an}的通项公式.
(2)当n=1时,b1=
+1=
,T1=
;当n≥2时,bn=
+n=
-
+n,由此利用分组求和法和裂项求和法能求出数列{bn}的前n项和Tn.
(2)当n=1时,b1=
| 1 |
| 2log24 |
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| (n+1)log22n |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)当n=1时,a1=S1=4,…(2分)
由Sn=2n+1,得Sn-1=2n,n≥2,
∴an=Sn-Sn-1=2n+1-2n =2n,n≥2.
∴an=
.…(6分)
(2)当n=1时,b1=
+1=
,∴T1=
,…(7分)
当n≥2时,
bn=
+n
=
+n=
-
+n,…(9分)
Tn=
+(
-
+
-
+…+
-
)+(2+3+4+…+n)
=
+(
-
+
-
+…+
-
)+(1+2+3+4+…+n)
=
-
+
,…(11分)
上式对于n=1也成立,
∴Tn=
-
+
.…(12分)
由Sn=2n+1,得Sn-1=2n,n≥2,
∴an=Sn-Sn-1=2n+1-2n =2n,n≥2.
∴an=
|
(2)当n=1时,b1=
| 1 |
| 2log24 |
| 5 |
| 4 |
| 5 |
| 4 |
当n≥2时,
bn=
| 1 |
| (n+1)log22n |
=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
Tn=
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 3 |
| 4 |
| 1 |
| n+1 |
| n(n+1) |
| 2 |
上式对于n=1也成立,
∴Tn=
| 3 |
| 4 |
| 1 |
| n+1 |
| n(n+1) |
| 2 |
点评:本题考查数列的通项公式的求法,考查为数列的前n项和的求法,解题时要认真审题,注意分组求和法和裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
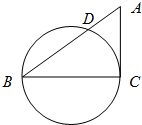
已知Rt△ABC中,∠C=90°,AB=5,BC=4,以BC为直径的圆交AB于D,则BD的长为( )

| A、4 | ||
B、
| ||
C、
| ||
D、
|
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:

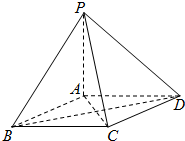 如图,四棱锥P-ABCD的俯视图是菱形ABCD,顶点P的投影恰好为A.
如图,四棱锥P-ABCD的俯视图是菱形ABCD,顶点P的投影恰好为A.