题目内容
解不等式：
＞0．
| 1 |
| mx-2 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：对参数m分m＜0、m=0、m＞0三类讨论，即可求得原不等式的解集．
解答：
解：
＞0?mx-2＞0，
当m=0时，-2＞0，这不可能，x∈∅；
当m＜0时，-mx＜-2，解得：x＜
；
当m＞0时，解得：x＞
；
∴当m＜0时，原不等式的解集为{x|x＜
}；
当m=0时，原不等式的解集为∅；
当m＞0时，原不等式的解集为{x|x＞
}．
| 1 |
| mx-2 |
当m=0时，-2＞0，这不可能，x∈∅；
当m＜0时，-mx＜-2，解得：x＜
| 2 |
| m |
当m＞0时，解得：x＞
| 2 |
| m |
∴当m＜0时，原不等式的解集为{x|x＜
| 2 |
| m |
当m=0时，原不等式的解集为∅；
当m＞0时，原不等式的解集为{x|x＞
| 2 |
| m |
点评：本题考查分式不等式的解法，着重考查分类讨论思想的应用，属于中档题．
练习册系列答案
相关题目
已知
=（2，-2
），
=（-7，0），则
与
的夹角为（ ）
| a |
| 3 |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
在△ABC中，若对任意的λ∈R，都有|
+λ
|≥|
|，则△ABC（ ）
| AB |
| AC |
| BC |
| A、一定为锐角三角形 |
| B、一定为钝角三角形 |
| C、一定为直角三角形 |
| D、可以为任意三角形 |
已知Rt△ABC中，∠C=90°，AB=5，BC=4，以BC为直径的圆交AB于D，则BD的长为（ ）
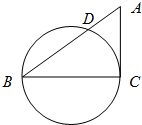
| A、4 | ||
B、
| ||
C、
| ||
D、
|
已知三棱柱ABC-A1B1C1侧棱与底面垂直，且其六个顶点都在球O的球面上，若AC=3，AB=4，CB=5，球O的半径为6，则OA与平面ABC所成的角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
