题目内容

10．若直线l1：mx+y-1=0，l2：4x+my+m-4=0，则“m=2”是“直线l1⊥l2”的（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件

分析 通过讨论m的范围，求出“直线l1⊥l2”的充要条件，从而得出答案．

解答 解：若m=0，则l1：y-1=0，l2：4x-4=0，垂直，
若m=0，则l1的斜率是-m，l2的斜率是-$\frac{4}{m}$，
而-m•（-$\frac{4}{m}$）=4≠-1，不垂直，
故若l1⊥l2，只需m=0，
故“m=2”是“直线l1⊥l2”的既不充分也不必要条件，
故选：D．

点评 本题考查了充分必要条件，考查直线的垂直，是一道基础题．

练习册系列答案
相关题目
19．已知函数f（x）=ex-2x．
（1）求函数f（x）的极值；
（2）证明：当x＞0时，ex＞x2；
（3）当x＞0时，方程f（x）=kx2-2x无解，求k的取值范围．
1．已知函数f（x）=ax3+cx+d（a≠0）是R上的奇函数，当x=1时f（x）取得极值-2．
（1）求a，c，d的值，并求f（x）的极大值；
（2）证明对任意x1，x2∈（-1，1），不等式|f（x1）-f（x2）|＜4恒成立．
18．若复数z满足z（1-i）=2，则z=（　　）
A．1-iB．1+iC．2-2iD．2+2i
5．函数f（x）在点x0处取得极值，则必有（　　）
A．f′（x0）=0B．f′（x0）＜0
C．f′（x0）=0且f″（x0）＜0D．f′（x0）或f′（x0）不存在
15．（1）直线kx-y+1=3k，当k变动时，所有直线都通过一个定点，求这个定点；
（2）过点P（1，2）作直线l交x、y轴的正半轴于A、B两点，求使$\overrightarrow{PA}$•$\overrightarrow{PB}$取得最大值时，直线l的方程．
2．已知函数f（x）=ax2+lnx（a为正实数），且f（x）的导函数f′（x）在x=$\frac{1}{2}$处取极小值．
（1）求实数a的值；
（2）设函数g（x）=3x+x2，若方程f（x）-g（x）+m=0在x∈[$\frac{1}{2}$，2]内恰有两个不相等的实数根，求实数m的取值范围（参考数据：ln2≈0.693）；
（3）记函数h（x）=f（x）-$\frac{3}{2}$x2-（b+1）x（b≥$\frac{3}{2}$）．设x1，x2（x2＞x1＞0）是函数h（x）的两个极值点，点A（x1，h（x1）），B（x2，h（x2）），直线AB的斜率为kAB．若kAB≤$\frac{r}{{x}_{1}{-x}_{2}}$对任意x2＞x1＞0恒成立，求实数r的最大值．
19．通过观察下面两等式的规律，请你写出一般性的命题：
sin230°+sin290°+sin2150°=$\frac{3}{2}$
sin25°+sin265°+sin2125°=$\frac{3}{2}$
sin2（α-60°）+sin2α+sin2（α+60°）=$\frac{3}{2}$．
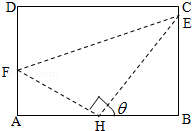20．如图，矩形ABCD的内接Rt△FHE，（H是直角顶点），H是AB的中点，E，F分别落在线段BC，AD上．已知AB=2，AD=$\sqrt{3}$，记∠BHE=θ．
（1）试将Rt△FHE的周长L表示为θ的函数，并写出定义域；
（2）当θ取何值时，Rt△FHE的周长L取最大值，并求出此时周长L．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网