题目内容
14.在坐标系中有两点P(2,3),Q(3,4).求(1)在y轴上求出一点M,使得MP+MQ的值最小;
(2)在x轴上求出一点N,使得NQ-NP的值最大.
分析 (1)作出P点关于y轴的对称点P′,连接P′Q与y轴的交点即为M;
(2)连接PQ并延长,与x轴交点就是N.
解答 解:(1)作出P点关于y轴的对称点P′,
连接P′Q与y轴的交点即为M;
∵P(2,3),Q(3,4).
∴P′的坐标为(-2,3),
故直线P′Q方程为:x-5y+17=0,
令x=0,则y=$\frac{17}{5}$,
即M点坐标为(0,$\frac{17}{5}$).
(2)连接PQ并延长,与x轴交点就是N.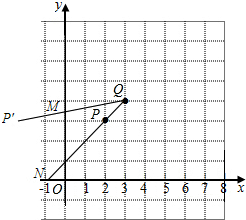
∵P(2,3),Q(3,4).
故直线PQ方程为:x-y+1=0,
令y=0,则x=-1,
即N点坐标为(-1,0)时,NQ-NP的值最大.
点评 本题考查的知识点是点到两定点距离和与距离差的最值问题,找到满足条件的点的位置是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.k∈Z时,$\frac{sin(kπ-α)•cos(kπ+α)}{sin[(k+1)π+α]•cos[(k+1)π+α]}$的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 与α取值有关 |
6.函数f(x)=x3,f′(x0)=6,则x0=( )
| A. | $\sqrt{2}$ | B. | $-\sqrt{2}$ | C. | ±1 | D. | $±\sqrt{2}$ |
3.设数列{an}的前n项和${S_n}=\frac{n}{n+2}$,则a6的值为( )
| A. | $-\frac{1}{28}$ | B. | $-\frac{1}{56}$ | C. | $\frac{1}{28}$ | D. | $\frac{1}{56}$ |
4.设a=7${\;}^{-\frac{1}{2}}$,b=($\frac{1}{7}$)${\;}^{-\frac{1}{3}}$,c=log7$\frac{1}{2}$,则下列关系中正确的是( )
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | b<c<a |
