题目内容
5．已知定义在R上的函数f（x）=|x+1|+|x-2|的最小值为a．（1）求a的值；
（2）解不等式f（x）＞4．
分析 （1）根据|x+1|+|x-2|≥|（x+1）-（x-2）|=3，求出f（x）的最小值；
（2）讨论x的取值范围，求出f（x）的解析式，再求不等式f（x）＞4的解集．
解答 解：（1）因为|x+1|+|x-2|≥|（x+1）-（x-2）|=3，
当且仅当-1≤x≤2时，等号成立，
所以f（x）的最小值等于3，即a=3；
（2）由（1）知，当-1≤x≤2时，f（x）=3，f（x）＞4不成立；
当x＜-1时，f（x）=-（x+1）-（x-2）=-2x+1，
不等式f（x）＞4化为-2x+1＞4，解得x＜-$\frac{3}{2}$；
当x＞2时，f（x）=（x+1）+（x-2）=2x-1，
不等式f（x）＞4化为2x-1＞4，解得x＞$\frac{5}{2}$；
所以，不等式f（x）＞4的解集为{x|x＜-$\frac{3}{2}$或x＞$\frac{5}{2}$}．
点评 本题考查了不等式的解法与应用问题，也考查了绝对值不等式的应用问题，是基础题目．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
16．已知向量$\overrightarrow a=（cosx-sinx，2cosx）$，$\overrightarrow b=（cosx+sinx，sinx）（x∈R）$，则函数$f（x）={（\overrightarrow a•\overrightarrow b）^2}-1$是（ ）
| A． | 周期为π的偶函数 | B． | 周期为π的奇函数 | ||
| C． | 周期为$\frac{π}{2}$的偶函数 | D． | 周期为$\frac{π}{2}$的奇函数 |
20．设函数$f（x）=cos（{πx-π}）+1，\;\;x∈（{\frac{1}{2}，\frac{3}{2}}）$，若关于x的方程2[f（x）]2-（2a+3）f（x）+3a=0有四个不同的实数解，则满足题意的实数a的取值范围是（ ）
| A． | （0，1） | B． | $（{0，\frac{3}{2}}）$ | C． | （1，2） | D． | $（{1，\frac{3}{2}}）∪（{\frac{3}{2}，2}）$ |
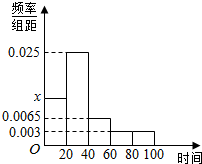某学校随机调查了部分学生的上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]