题目内容
5.已知函数f(x)=ax-lnx,(a∈R),(1)是否存在实数a,当x∈(0,e](e是自然常数)时,函数f(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(2)当x∈(0,e]时,证明:e2x2-$\frac{5}{2}$x>(x+1)lnx.
分析 (1)求出函数f(x)的导数,通过讨论a的范围,求出函数的单调区间,从而求出满足条件的a的值即可;
(2)令F(x)=e2x-lnx,求出F(x)的最小值,令ω(x)=$\frac{lnx}{x}$+$\frac{5}{2}$,求出ω(x)的最大值,从而证出结论即可.
解答 解:(1)假设存在实数a,使f(x)=ax-lnx,(x∈(0,e])有最小值3,$f'(x)=\frac{ax-1}{x}$
①当a≤0时,f(x)在(0,e]上单调递减,f(x)min(x)=f(e)=ae-1=3,
a=$\frac{4}{e}$(舍去),
②当0<$\frac{1}{a}$<e时,f(x)在(0,$\frac{1}{a}$)上单调递减,在($\frac{1}{a}$,e]上单调递增,
∴$f{(x)_{min}}=f(\frac{1}{a})=1+lna=3$,a=e2,满足条件.
③当$\frac{1}{a}$≥e时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,
a=$\frac{4}{e}$(舍去),
综上,存在实数a=e2,使得x∈(0,e]时,f(x)有最小值3;
(2)令F(x)=e2x-lnx,由(1)得:F(x)min=3,
令ω(x)=$\frac{lnx}{x}$+$\frac{5}{2}$,则ω′(x)=$\frac{1-lnx}{{x}^{2}}$,
令ω′(x)>0,解得:0<x<e,故ω(x)在(0,e]递增,
∴ω(x)max=ω(e)=3,
∴e2x2-$\frac{5}{2}$x>(x+1)lnx.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及放假分类讨论思想,转化思想,是一道中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
16.直线x+y-2=0和x-y-4=0的交点为( )
| A. | (3,-1) | B. | (-3,-1) | C. | (-3,1) | D. | (3,1) |
20.己知函数f(x)=x3-3x,若过点A(1,m)可作曲线y=f(x)的三条切线,则实数m的取值范围是( )
| A. | -1<m<1 | B. | -4<m<4 | C. | -1<m<-2 | D. | -3<m<-2 |
17.已知偶函数f(x)的定义域为(-∞,0)∪(0,+∞),且对任意正实数x1,x2(x1≠x2)恒有(x1-x2)[f(x1)-f(x2)]>0,则一定有( )
| A. | f(3)>f(-3) | B. | f(-3)>f(-5) | C. | f(-30.3)>f(0.33) | D. | f(log32)>f(-log23) |
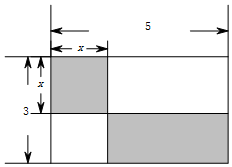 如图,一个长为5、宽为3的矩形被平行于边的两条直线所分割,其中矩形的左上角是一个是一个边长为x的正方形
如图,一个长为5、宽为3的矩形被平行于边的两条直线所分割,其中矩形的左上角是一个是一个边长为x的正方形