题目内容
12.化简:$\frac{cos(3π-θ)cot(π+θ)tan(-θ)}{sin(π-θ)cot(3π-θ)}$=-1.分析 根据诱导公式和同角的三角函数的关系化简即可.
解答 解:$\frac{cos(3π-θ)cot(π+θ)tan(-θ)}{sin(π-θ)cot(3π-θ)}$=$\frac{-cosθcotθ(-tanθ)}{sinθ(-cotθ)}$=-1,
故答案为:-1.
点评 本题考查了诱导公式和同角的三角函数的关系,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20.曲线y=x3-$\sqrt{3}x$+2上的任意一点P处切线的倾斜角的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$) | B. | [$\frac{2π}{3}$,π) | C. | [0,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{2π}{3}$] | D. | [0,$\frac{π}{2}$)∪[$\frac{2π}{3}$,π) |
17.为了得到函数y=lg$\frac{x+3}{10}$的图象,只需把函数y=lgx的图象上所有的点( )
| A. | 向左平移3,向上平移1个单位 | B. | 向右平移3,向上平移1个单位 | ||
| C. | 向左平移3,向下平移1个单位 | D. | 向右平移3,向下平移1个单位 |
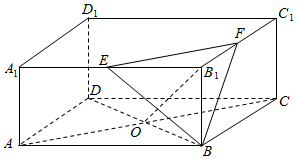 如图,已知长方体ABCD-A1B1C1D1中AB=BC=2,AA1=1,点E,F分别是A1B1,B1C1的中点,点O是AB与BD的交点.
如图,已知长方体ABCD-A1B1C1D1中AB=BC=2,AA1=1,点E,F分别是A1B1,B1C1的中点,点O是AB与BD的交点.