题目内容
2.已知数列{an}是等差数列,Sn是其前n项和,若s6=3,S12-S6=9,则S18=27.分析 利用等差数列{an}的性质可得:s6,S12-S6,S18-S12成等差数列,即可得出.
解答 解:由等差数列{an}的性质可得:其前n项和Sn,s6,S12-S6,S18-S12成等差数列,
∴2×9=3+S18-S12,S12=9+3=12.
∴S18=27.
故答案为:27.
点评 本题考查了等差数列的前n项和的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.在等比数列{an}中,设Sn为其前n项和,若a1a3=4,且S3=-3,则S4=( )
| A. | 31 | B. | -23 | C. | -5或$\frac{5}{2}$ | D. | 5或-$\frac{5}{2}$ |
17.已知△ABC中,a=3,b=3$\sqrt{3}$,A=30°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
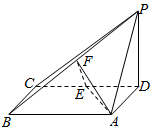 四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点.