题目内容
14.已知定义域为R的函数f(x)=$\frac{{-{2^x}+b}}{{{2^{x+1}}+a}}$是奇函数.(Ⅰ)求a,b的值;
(Ⅱ)已知f(x)在定义域上为减函数,若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0(k为常数)恒成立.求k的取值范围.
分析 (Ⅰ)利用奇函数定义f(-x)=-f(x)中的特殊值求a,b的值;
(Ⅱ)首先确定函数f(x)的单调性,然后结合奇函数的性质把不等式f(t2-2t)+f(2t2-k)<0转化为关于t的一元二次不等式,最后由一元二次不等式知识求出k的取值范围.
解答 解:(Ⅰ)f(x)是定义在R的奇函数,所以f(-x)=-f(x)
令x=0,f(0)=-f(0),f(0)=0
令x=1,f(-1)=-f(1),
所以$\left\{\begin{array}{l}{\frac{{-{2^0}+b}}{2'+a}=0}\\{\frac{{-{2^{-1}}+b}}{{{2^0}+a}}=-\frac{{-{2^1}+b}}{{{2^2}+a}}}\end{array}$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}$;
(Ⅱ)经检验,当a=2,b=1时,f(x)为奇函数.
所以f(t2-2t)<-f(2t2-k)
因为f(x)是奇函数,所以f(t2-2t)<f(k-2t2)
因为f(x)在R上单调减,所以t2-2t>k-2t2
即3t2-2t-k>0在R上恒成立,所以△=4+4•3k<0
所以k<-$\frac{1}{3}$,即k的取值范围是(-∞,-$\frac{1}{3}$).
点评 本题主要考查函数奇偶性与单调性的综合应用;同时考查一元二次不等式恒成立问题的解决策略.

练习册系列答案
相关题目
4.已知实数m,n满足$\frac{5+mi}{n-2i}$=4+6i,则在复平面内,复数z=m+ni所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知x,y∈R,i为虚数单位,且(x-2)i-y=-1+i,则(1+i)x+y的值为( )
| A. | 4 | B. | 4+4i | C. | -4 | D. | 2i |
9.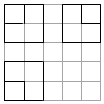 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
10.福利彩票“双色球”中红色球的号码由编号为01,02,…,33的33个个体组成,小明利用下面的随机数表选取6组数作为6个红色球的编号,选取方法是从随机数表第1行的第7列数字开始由左到右依次读取数据,则选出来的第3个红色球的编号为( )
| 49 54 43 54 15 37 17 93 39 78 87 35 20 96 43 84 17 34 91 64 |
| 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
| A. | 06 | B. | 17 | C. | 20 | D. | 24 |