题目内容
13.已知P为抛物线y2=4x上一个动点,Q为圆x2+(y-4)2=1上一个动点,当点P到点Q的距离与点P到抛物线的准线距离之和最小时,P点的横坐标为( )| A. | $\frac{\sqrt{17}}{8}$ | B. | $\frac{9-\sqrt{17}}{8}$ | C. | $\frac{9}{8}$ | D. | $\sqrt{17}$ |
分析 先根据抛物线方程求得焦点坐标,根据圆的方程求得圆心坐标,根据抛物线的定义可知P到准线的距离等于点P到焦点的距离,进而问题转化为求点P到点Q的距离与点P到抛物线的焦点距离之和的最小值,求出直线FC的方程与抛物线方程联立求解即可.
解答 解:抛物线y2=4x的焦点为F(1,0),圆x2+(y-4)2=1的圆心为C(0,4),
根据抛物线的定义可知点P到准线的距离等于点P到焦点的距离,
进而推断出当P,Q,F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小,
此时直线FC的方程为:4x+y-4=0,
可得$\left\{\begin{array}{l}{{y}^{2}=4x}\\{4x+y-4=0}\end{array}\right.$,消去y,可得4x2-9x+4=0,解得x=$\frac{9-\sqrt{17}}{8}$,x=$\frac{9+\sqrt{17}}{8}$(舍去)
故选:B.
点评 本题主要考查了抛物线的应用.考查了学生转化和化归,数形结合等数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知实数m,n满足$\frac{5+mi}{n-2i}$=4+6i,则在复平面内,复数z=m+ni所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.“平面α内的两条直线与平面β都平行”是“平面α与平面β平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
9.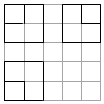 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
 如图,三棱柱ABC-A1B1C1所有的棱长均为2,A1B=$\sqrt{6}$,A1B⊥AC.
如图,三棱柱ABC-A1B1C1所有的棱长均为2,A1B=$\sqrt{6}$,A1B⊥AC.