题目内容

在平面直角坐标系中，已知O（0，0）、A（2，3）、B（-4，7），则向量
OA
在向量
OB
方向上的投影等于
 
．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的模的公式和数量积的坐标表示，结合向量
OA
在向量
OB
方向上的投影为
OA
•
OB
|
OB
|
，计算即可得到．
解答： 解：由于O（0，0）、A（2，3）、B（-4，7），
则
OA
=（2，3），
OB
=（-4，7），
OA
•
OB
=2×（-4）+3×7=13，
|
OB
|=
16+49
=
65
，
则向量
OA
在向量
OB
方向上的投影为
OA
•
OB
|
OB
|
=
13
65
=
65
5
．
故答案为：
65
5
．
点评：本题考查向量的数量积的坐标表示和向量的模的公式，考查向量的投影的概念，属于基础题．
练习册系列答案
相关题目
在平面直角坐标系中，以坐标原点为极点，以x轴正半轴为极轴，建立极坐标系，得到曲线C的极坐标方程是ρ=4sinθ
（Ⅰ）写出曲线C的标准方程及其参数方程；
（Ⅱ）在平面直角坐标系中，对于两点P（x1，y1），Q（x2，y2），记δ=|x1-x2|+|y1-y2|，点P（2，4），Q在曲线C上运动，求δ的取值范围．
观察下列式子：1+
1
22
＜
3
2
，1+
1
22
+
1
32
＜
5
3
，1+
1
2 
+
1
32
+
1
42
＜
7
4
，…根据以上式子可以猜想：1+
1
22
+
1
32
+
1
42
+…+
1
20152
＜
 
．
把正整数排列陈如图甲的三角形数阵，然后擦去第偶数行中的奇数和第奇数行中的偶数，得到如图乙的三角形数阵，再把图乙中的数按从小到大的顺序排出一列，得到数列{an}．

（1）a32=
 
；
（2）若an=2080，则n
 
．
过双曲线
x2
3
-y2=1的两焦点作实轴的垂线，分别与渐近线交于A、B、C、D四点．则矩形ABCD的面积为
 
．
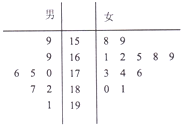第117届中国进出口商品交易会（简称2015年春季交广会）将于2015年4月15日在广州市举行，为了搞好接待工作，组委会在广州某大学分别招募8名男志愿者和12名女志愿者，现将这20名志愿者的身高组成如茎叶图（单位：m），若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”．
（1）计算男志愿者的平均身高（保留一位小数）；
（2）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5个人选2人，求至少有1人是“高个子”的概率．
下列四个函数：①y=x+1；②y=x-1；③y=x2-1；④y=
1
x
，其中定义域与值域相同的是（　　）
A、①②③B、①②④
C、②③D、②③④
若直线l1，l2的方向向量分别为
v1
=（1，2，3），
v2
=（-
1
2
，-1，-
3
2
），则l1，l2的位置关系是（　　）
A、垂直B、重合
C、平行D、平行或重合
斜率为2的直线l过双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点，且与双曲线的左右两支都相交，则双曲线的离心率e的取值范围是（　　）
A、[2，+∞）
B、（1，
3
）
C、(1，
5
)
D、（
5
，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网