题目内容
若方程(1-a)sin2x+2sinxcosx-(2+a)cos2x=0有无数个解,则a取值范围为 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:根据2倍角公式原方程可化为,sin2x-
cos2x=a+
,即
sin(2x-θ)=a+
,其中tanθ=
,由题意方程有无数个解,根据三角函数的值域,得到不等式-
≤a+
≤
,解得即可.
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答:
解:∵(1-a)sin2x+2sinxcosx-(2+a)cos2x=0,
∴sin2x-asin2x+sin2x-2cos2x-acos2x=0.
∴(1-cos2x)+sin2x-(cos2x+1)-a=0,
∴sin2x-
cos2x=a+
,
∴
sin(2x-θ)=a+
,其中tanθ=
,
∵-1≤sin(2x-θ)≤1,
∴-
≤
sin(2x-θ)≤
,
∴-
≤a+
≤
,
∴-
-
≤a≤
-
,
即a取值范围为[-
,
]
∴sin2x-asin2x+sin2x-2cos2x-acos2x=0.
∴(1-cos2x)+sin2x-(cos2x+1)-a=0,
∴sin2x-
| 3 |
| 2 |
| 1 |
| 2 |
∴
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵-1≤sin(2x-θ)≤1,
∴-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
即a取值范围为[-
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了三角函数的化简,主要是2倍角公式,以及方程的解得问题,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
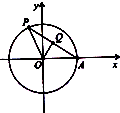 如图,A是单位圆与x轴正半轴的交点,点P在该单位圆上,∠AOP=θ(0<θ<π),点Q满足
如图,A是单位圆与x轴正半轴的交点,点P在该单位圆上,∠AOP=θ(0<θ<π),点Q满足| PQ |
| QA |
| OA |
| OQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|