题目内容
函数f（x）=x3+x在x=1处的切线为（ ）
| A、y=4x+4 |
| B、y=4x-2 |
| C、y=4-4x |
| D、y=4-2x |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出函数f（x）在点x=1处的导数，也就是切线的斜率，再利用点斜式求出切线方程．
解答：
解：∵f（x）=x3+x，
∴f′（x）=3x2+1．
∴x=1时，切线的斜率为4．
当x=1时，f（x）=2，
利用点斜式，求出切线方程为y=4x-2．
故选B．
∴f′（x）=3x2+1．
∴x=1时，切线的斜率为4．
当x=1时，f（x）=2，
利用点斜式，求出切线方程为y=4x-2．
故选B．
点评：本题比较简单，主要应用导数的几何意义，求出切线方程．
练习册系列答案
相关题目
设变量x，y满足
，则目标函数z=2x+y的最小值（ ）
|
| A、25 | B、23 | C、7 | D、5 |
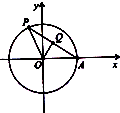如图，A是单位圆与x轴正半轴的交点，点P在该单位圆上，∠AOP=θ（0＜θ＜π），点Q满足| PQ |
| QA |
| OA |
| OQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知平向向量
，
满足：|
|=1，|
|=6，
•（
-
）=2，则向量
与向量
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
定积分
（
-x）dx等于（ ）
| ∫ | 1 0 |
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某算法的程序框如图所示，若输出结果为
，则输入的实数x的值是（ ）
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
| D、4 |
若102x=25，则x=（ ）
A、lg
| ||
| B、lg5 | ||
| C、2lg5 | ||
D、2lg
|
复数z=3-2i所对应的点位于复平面的（ ）
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |