题目内容
13.已知集合A={θ|cosθ<sinθ,0≤θ<2π},B={θ|tanθ<sinθ},则A∩B={θ|$\frac{π}{2}$<θ<π}.分析 先分别同集合,B,由此能求出A∩B.
解答 解:∵集合A={θ|cosθ<sinθ,0≤θ<2π}={θ|$\frac{π}{4}<θ<\frac{5π}{4}$},
B={θ|tanθ<sinθ}={θ|$\frac{π}{2}<θ<π$或$\frac{3π}{2}$<θ<2π},
∴A∩B={θ|$\frac{π}{2}$<θ<π}.
故答案为:{θ|$\frac{π}{2}$<θ<π}.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义、三角函数性质的合理运用.

练习册系列答案
相关题目
3.已知a,b,c是锐角△ABC中的角A、B、C的对边,若$B=\frac{π}{4}$,则$\frac{acosC-ccosA}{b}$的取值范围为( )
| A. | (-1,1) | B. | $(-\frac{1}{2},\frac{1}{2})$ | C. | $(-\sqrt{2},\sqrt{2})$ | D. | $(-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2})$ |
4.执行如图所示的程序框图,若$a=\frac{9}{4}$,则输出S的值为( )
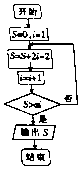

| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
1.曲线M的方程为$\sqrt{{{(x-1)}^2}+{y^2}}+\sqrt{{{(x+1)}^2}+{y^2}}$=4,直线y=k(x+1)交曲线M于A,B两点,点C(1,0),则△ABC的周长为( )
| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |
8.A,B,C是球O上的三点,AB=5,AC=3,BC=4,球O的直径等于13,则球心O到平面ABC的距离为( )
| A. | $2\sqrt{3}$ | B. | 6 | C. | 9 | D. | 12 |
18.要得到函数f(x)=sin2x,x∈R,只需将函数g(x)=cos2x,x∈R的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
3.定义在R上的函数f(x)的导函数为f'(x),f(x)的图象关于直线x=1对称,且(x-1)f'(x)<0,若x1<x2,且x1+x2>2,则f(x1)与f(x2)的大小关系是( )
| A. | f(x1)>f(x2) | B. | f(x1)<f(x2) | C. | f(x1)=f(x2) | D. | 不确定 |