题目内容
已知函数f(x)=
sin2x+
cos2x+a-2,
(1)求函数f(x)的单调递增区间;
(2)设函数f(x)在[0,
]上的最小值为-
,求函数f(x)(x∈R)的值域.
| ||
| 2 |
| 3 |
| 2 |
(1)求函数f(x)的单调递增区间;
(2)设函数f(x)在[0,
| π |
| 2 |
| 3 |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)直接结合三角恒等变换公式化简,然后,借助于三角函数的单调性求解其单调区间;
(2)结合[0,
],然后,借助于三角函数的单调性确定其值域.
(2)结合[0,
| π |
| 2 |
解答:
解:(1)∵函数f(x)=
sin2x+
cos2x+a-2,
∴f(x)=
sin(2x+
)+a-2,
其单调递增区间为[-
+kπ,
+kπ],k∈Z.
(2)∵x∈[0,
]⇒2x+
∈[
,
],
则f(x)min=
•(-
)+a-2=-
⇒a=2,
∴f(x)∈[-
,
].
∴函数f(x)(x∈R)的值域[-
,
].
| ||
| 2 |
| 3 |
| 2 |
∴f(x)=
| 3 |
| π |
| 3 |
其单调递增区间为[-
| 5π |
| 12 |
| π |
| 12 |
(2)∵x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
则f(x)min=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴f(x)∈[-
| 3 |
| 3 |
∴函数f(x)(x∈R)的值域[-
| 3 |
| 3 |
点评:本题重点考查了三角恒等变换公式、三角函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
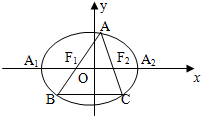 如图:A1、A2是椭圆
如图:A1、A2是椭圆